Robust TruncatedL1-L2Total Variation Sparse Restoration Models

doi:10.12141/j.issn.1000-565X.220485

Abstract

Abstract:

In addition to Gaussian noise, there is sparse noise with impulsive properties in the signal acquisition process. The common robust sparse signal recovery models can recover the original sparse signal under sparse noise environment. However, in many practical applications, the structural sparsity of the original signal, for example, gradient sparsity needs to be considered. In order to recover the sparse structure of the original high-dimensional signal from the coexistence of sparse noise and Gaussian noise, this paper proposed two nonconvex and nonsmooth optimization models based on truncated L₁-L₂ total variation (TV) and 3D truncated L₁-L₂ TV, respectively. These optimization models were solved by the proximal alternating linearized minimization algorithm with extrapolation, and the sub-problems involved were solved by the proximal convex difference algorithm with extrapolation. Under the assumption that the potential function has Kurdyka-Lojasiewicz (KL) property, the convergence analysis of these algorithms was given. The numerical experiments test grey images with Gaussian noise, color images with mixed noise, grey video with mixed noise and so on. The peak signal-to-noise ratio (PSNR) was used as the evaluation criterion for recovered quality. The experimental results show that the new models can correctly recover the original structured sparse signal, and have better PSNR values in the same noisy environment.

Key words: robust compressed sensing, truncated total variation, nonconvex and nonsmooth optimization, sparse noise, structural sparse

CLC Number:

TP391.41

HAN Le, JIANG Yihua. Robust TruncatedL1-L2Total Variation Sparse Restoration Models[J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(5): 45-53.

Figures/Tables 9

Fig.1

Table 1

PSNR， SSIM and running time of recovering grey images with Gaussian noise"

图像序号	PSNR/dB			SSIM/dB			运行时间/s
图像序号	$L 1 / 2$	TVT0	TVT1	$L 1 / 2$	TVT0	TVT1	$L 1 / 2$	TVT0	TVT1
1	26.82	25.62	27.16	0.760 0	0.506 9	0.802 8	0.02	0.01	45.25
2	28.10	26.72	30.19	0.760 0	0.438 4	0.818 0	0.02	0.01	43.30
3	26.84	26.96	29.08	0.800 0	0.508 9	0.880 7	0.02	0.01	44.01
4	28.90	27.68	31.21	0.820 0	0.692 1	0.896 1	0.02	0.01	46.86
5	26.92	26.51	29.38	0.860 0	0.807 3	0.910 0	0.10	0.05	282.85
6	23.98	24.90	24.90	0.860 0	0.806 7	0.834 0	0.10	0.05	733.15

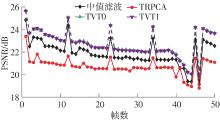
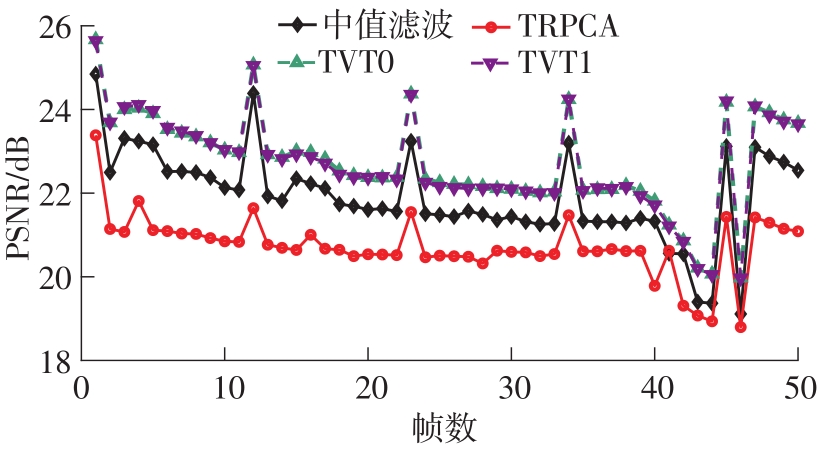
Table 1

Fig.2

Table 2

Table 3

Fig.3

Table 4

Table 5

Fig.4

References 25

1	WANG C， TAO M， NAGY J G，et al ．Limited-angle CT reconstruction via the L₁/L₂ minimization ［J］．SIAM Journal on Imaging Sciences，2021，14（2）：749-777.
2	FANNJIANG A， LIAO W ．Coherence pattern-guided compressive sensing with unresolved grids ［J］．SIAM Journal on Imaging Sciences，2012，5（1）：179-202.
3	LAI M J， XU Y， YIN W ．Improved iteratively reweighted least squares for unconstrained smoothed l q minimization ［J］．SIAM Journal on Numerical Analysis，2013，51（2）：927-957.
4	BIAN W， CHEN X J ．A smoothing proximal gradient algorithm for nonsmooth convex regression with cardinality penalty［J］．SIAM Journal on Numerical Analysis，2020，58（1）：858-883.
5	YOU J， JIAO Y， LU X，et al ．A nonconvex model with minimax concave penalty for image restoration ［J］．Journal of Scientific Computing，2019，78（2）：1063-1086.
6	THI H A L， PHAMDINH T ．DC programming and DCA：thirty years of developments ［J］．Mathematical Programming，2018，169：5-68.
7	ARAGÓN ARTACHO F J， VUONG P T ．The boosted difference of convex functions algorithm for nonsmooth functions ［J］．SIAM Journal on Control and Optimization，2020，30（1）：980-1006.
8	LI W J， BIAN W， TOH K C ．DC algorithms for a c‍l‍ass of sparse group l 0 regularized optimization problems ［EB/OL］．（2021-09-11）［2022-01-03］．.
9	MA T H， LOU Y F， HUANG T Z ．Truncated l 1 - 2 mo‍dels for sparse recovery and rank minimization ［J］．SIAM Journal on Imaging Sciences，2017，10（3）：1346-1380.
10	LIU T X， PONG T K， TAKED A ．A refined convergence analysis of pDCA _e with applications to simultaneous sparse recovery and outlier detection ［J］．Computational Optimization and Applications，2019，73：69-100.
11	CARRILLO R E， RAMIREZ A B， ARCE G R，et al ．Robust compressive sensing of sparse signals：a review ［J］．EURASIP Journal on Advances in Signal Processing，2016，2016：108/1-17.
12	BABAHREINIAN M， TRON R ．A computational theory of robust localization verifiability in the presence of pure outlier measurements ［EB/OL］．（2019-10-12）［2021-05-03］．.
13	GAO X， CAI X， HAN D ．A Gauss-Seidel type inertial proximal alternating linearized minimization for a class of nonconvex optimization problems ［J］．Journal of Global Optimization，2020，76：863-887.
14	BOLTE J， DANIILIDIS A， LEWIS A S，et al ．Clark subgradients of stratifiable functions ［J］．SIAM Journal on Optimization，2007，18（2）：556-572.
15	CHAMBOLLE A ．An algorithm for total variation m‍inimization and applications ［J］．Journal of Mathematical Imaging & Vision，2004，20：89-97.
16	XU Y， HUANG T Z， LIU J，et al ．Split Bregman iteration algorithm for image deblurring using fourth-order total bounded variation regularization model ［J］．Journal of Applied Mathematics，2013，2013：238561/1-11.
17	CHAMBOLLE A， EHRHARDT M J， RICHTÀRIK P，et al ．Stochastic primal-dual hybrid gradient algorithm with arbitrary sampling and imaging applications ［J］．SIAM Journal on Optimization，2018，28（4）：2783-2808.
18	HINTERRMULLER M， STADLER G ．An infeasible primal-dual algorithm for total bounded variation-based inf-convolution-type image restoration ［J］．SIAM Journal on Scientific Computing，2006，28（1）：1-23.
19	CHEN C， MICHAEL K N， ZHAO X ．Alternating direction method of multipliers for nonlinear image restoration problems ［J］．IEEE Transaction on Image Processing，2015，24（1）：32-43.
20	GOLDFARB D， YIN W ．Parametric maximum flow algorithms for fast total variation minimization ［J］．SIAM Journal on Scientific Computing，2009，31（5）：3712-3743.
21	BARBERO L，SRA S ．Modular proximal optimizatio‍‍n‍ for multidimensional total-variation regularization ［J］．Journal of Machine Learning Research，2018，19（1）：1-82.
22	NOCEDAL J， WRIGHT S T ．Numerical optimization［M］．New York：Springer，1999：510.
23	MARTIN D， FOWLKES C，TAL D，et al ．A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics［C］∥ Proceedings of the Eighth IEEE International Conference on Computer Vision．Vancouver：IEEE，2001：416-423.
24	LU C， FENG J， CHEN Y，et al ．Tensor robust principal component analysis with a new tensor nuclear norm ［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2020，42（4）：925-938.
25	BIOUCAS-DIAS J M， FIGUEIREDO M， OLIVEIRA J P ．Total variation-based image deconvolution：a majorization minimization approach［C］∥ Proceedings of 2006 IEEE International Conference on Acoustics Speech and Signal Processing．Toulouse：IEEE，2006：861-864.

图像序号	含稀疏噪声的PSNR/dB			含混合噪声的PSNR/dB
图像序号	TRPCA	TVT0	TVT1	TRPCA	TVT0		TVT1
1	23.28	24.38	24.71	19.18	21.48	21.74
2	24.49	24.67	24.98	19.21	21.40	21.40
3	27.70	28.00	27.50	20.68	23.22	22.71
4	24.43	24.62	24.40	19.52	21.36	21.08
5	29.73	30.11	29.87	21.79	21.79	23.73
6	31.52	31.89	29.83	20.63	21.12	20.75

图像序号	噪声	每次迭代的平均运行时间/s			总迭代次数
图像序号	噪声	TRPCA	TVT0	TVT1	TRPCA	TVT0	TVT1
1	稀疏噪声	0.002	0.993	4.956	43	150	150
2		0.001	0.960	3.815	42	150	150
3		0.001	1.025	3.962	43	84	113
4		0.002	1.043	3.909	43	127	150
5		0.001	0.970	4.029	44	89	143
6		0.001	1.020	3.720	43	116	101
1	混合噪声	0.001	1.149	3.474	40	150	1
2		0.002	1.127	3.087	40	150	1
3		0.001	1.099	3.071	40	150	1
4		0.002	1.056	3.140	40	150	1
5		0.001	1.119	3.092	41	150	1
6		0.001	1.108	3.257	40	150	150

帧数	PSNR/dB
帧数	TRPCA	中值滤波	TVT0	TVT1
1	23.38	24.85	25.67	25.64
7	21.03	22.52	23.44	23.48
13	20.77	21.93	22.92	22.92
18	20.65	21.74	22.53	22.45
24	20.47	21.51	22.34	22.26
30	20.60	21.44	22.10	22.10
36	20.61	21.32	22.09	22.12
42	19.31	20.55	20.86	20.84
48	21.29	22.88	23.93	23.86

[1]	HU Guanghua, OU Meitong, LI Zhendong. Multi-Object Recognition and 6-DoF Pose Estimation Based on Synthetic Datasets [J]. Journal of South China University of Technology(Natural Science Edition), 2024, 52(4): 42-50.
[2]	LUO Yutao, GAO Qiang. Traffic Sign Detection Based on Channel Attention and Feature Enhancement [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(12): 64-72.
[3]	LI Haiyan, YIN Haolin, LI Peng, et al.. Image Inpainting Algorithm Based on Dense Feature Reasoning and Mix Loss Function [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(9): 99-109.
[4]	LIU Yijun, WANG Jiada, ZHONG Shijie, et al.. Fast Multi-View Clustering Based on Uniform Label Matrix [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(9): 110-119.
[5]	WANG Shiyong, QIAN Guokang, LI Di, et al.. Real-Time Template Matching Method for Edge Features [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(9): 1-10.
[6]	LIN Zhijian, DING Yongqiang, YANG Xiuzhi, et al. Parallel Pipeline Hardware Design of Intra Rate-Distortion Optimization Prediction Mode in HEVC [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(5): 95-103.
[7]	MA Biyun, WU Gang, LIU Jiaojiao, et al. Low Complexity Blood Flow Velocity Estimation Algorithm via Sparse Pulse Sampling [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(5): 63-69.
[8]	YI Qingming, LÜ Renyi, SHI Min, et al. Lightweight Object Detection Combined with Multi-Scale Dilated-Convolution and Multi-Scale Deconvolution [J]. Journal of South China University of Technology(Natural Science Edition), 2022, 50(12): 41-48.
[9]	HE Kai, LIU Zhiguo, LI Dashuang, et al. Non-rigid Point Set Registration Using Neighborhood Structure and Driving Force Criterion [J]. Journal of South China University of Technology(Natural Science Edition), 2022, 50(4): 73-80.
[10]	ZHANG Yan, GAO Zijian, XU Changkang, et al. Classification Method of Tactile Pressure Footprint Based on Fusion Distribution Graph Network [J]. Journal of South China University of Technology (Natural Science Edition), 2022, 50(1): 91-100.
[11]	HU Guanghua, WANG Ning, HE Wenliang, et al. Unsupervised Surface Defect Detection Method Based on Image Inpainting [J]. Journal of South China University of Technology (Natural Science Edition), 2021, 49(7): 76-85,124.
[12]	ZHANG Yan, WU Luotian, WANG Nian, et al. 2D Footprint Classification Based on Multiple-Module Relation Network [J]. Journal of South China University of Technology (Natural Science Edition), 2021, 49(6): 66-76.
[13]	YANG Chunling LING Xi. Two-Stage Multi-Hypothesis Network for Compressed Video Sensing Reconstruction Algorithms Based on Deep Learning [J]. Journal of South China University of Technology (Natural Science Edition), 2021, 49(6): 88-99.
[14]	GENG Qinghua, LIU Weiming. A Fast and Stable Algebraic Solution to Perspective-Three-Point Problem [J]. Journal of South China University of Technology(Natural Science Edition), 2021, 49(1): 58-64,73.
[15]	ZHENG Sifan, WANG Weixing, HE Zhanhua, et al. Research on Swing Amplitude Detection of Automobile Wiper with Two Granularity Optical Flow Manifold Learning#br# [J]. Journal of South China University of Technology (Natural Science Edition), 2020, 48(1): 123-132.