Journal of South China University of Technology(Natural Science Edition) ›› 2024, Vol. 52 ›› Issue (7): 39-52.doi: 10.12141/j.issn.1000-565X.230610
Special Issue: 2024年电子、通信与自动控制技术
• Electronics, Communication & Automation Technology • Previous Articles Next Articles
Probability Density Function Shape Control Method for Nonlinear Stochastic Systems Based on Compactly Supported Multi-Variable Polynomials
WANG Lingzhi1(), ZHANG Kun1, QIAN Fucai2
- 1.School of Automation, Xi’an University of Posts and Telecommunication, Xi’an 710121, Shaanxi, China
2.School of Automation and Information Engineering, Xi’an University of Technology, Xi’an 710048, Shaanxi, China
-
Received:2023-09-28Online:2024-07-25Published:2024-02-29 -
About author:王玲芝(1981—),女,博士,教授,主要从事随机控制、复杂系统的建模与优化控制、风能资源评估与预测、雷达目标散射特性等研究。E-mail: wlzmary@126.com -
Supported by:the National Natural Science Foundation of China(62073259)
CLC Number:
Cite this article
WANG Lingzhi, ZHANG Kun, QIAN Fucai. Probability Density Function Shape Control Method for Nonlinear Stochastic Systems Based on Compactly Supported Multi-Variable Polynomials[J]. Journal of South China University of Technology(Natural Science Edition), 2024, 52(7): 39-52.
share this article
Table 2
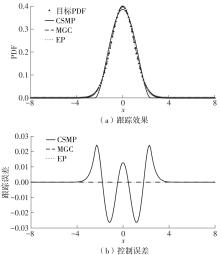
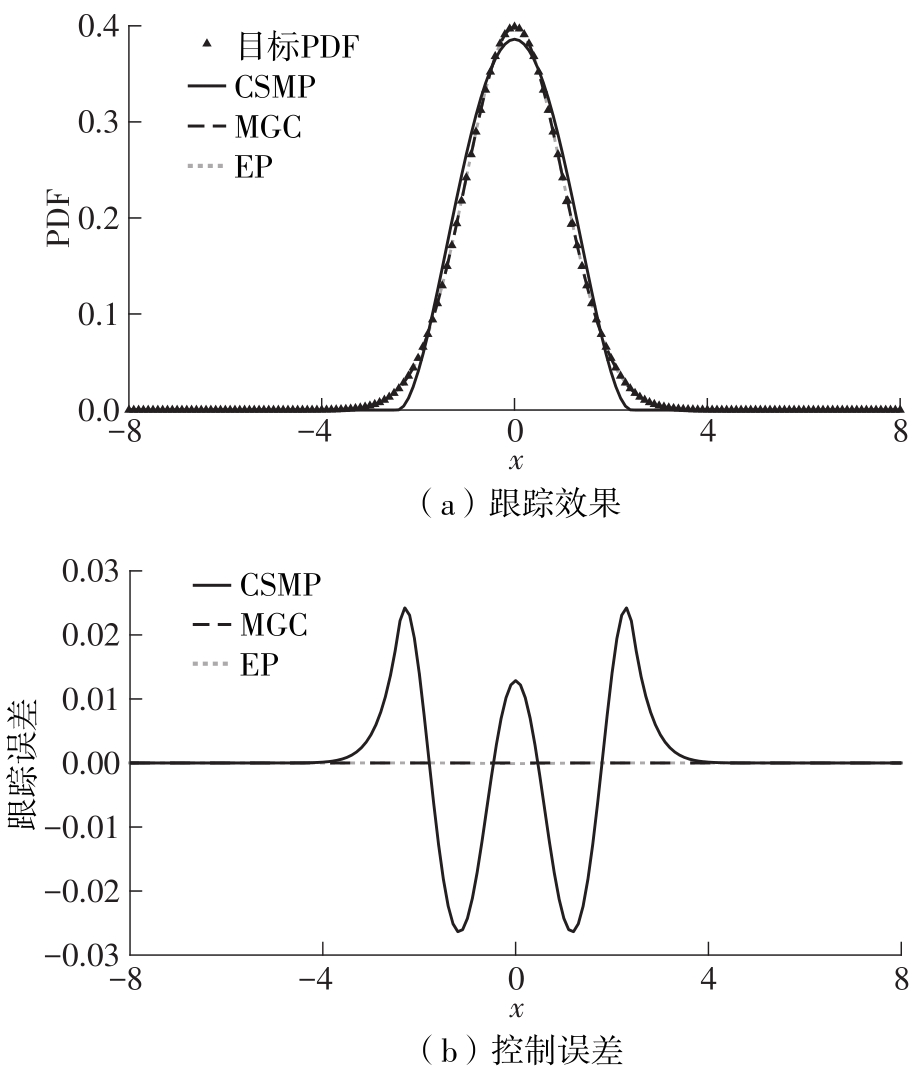
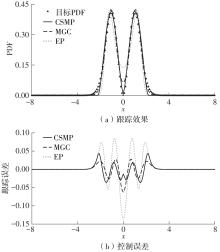
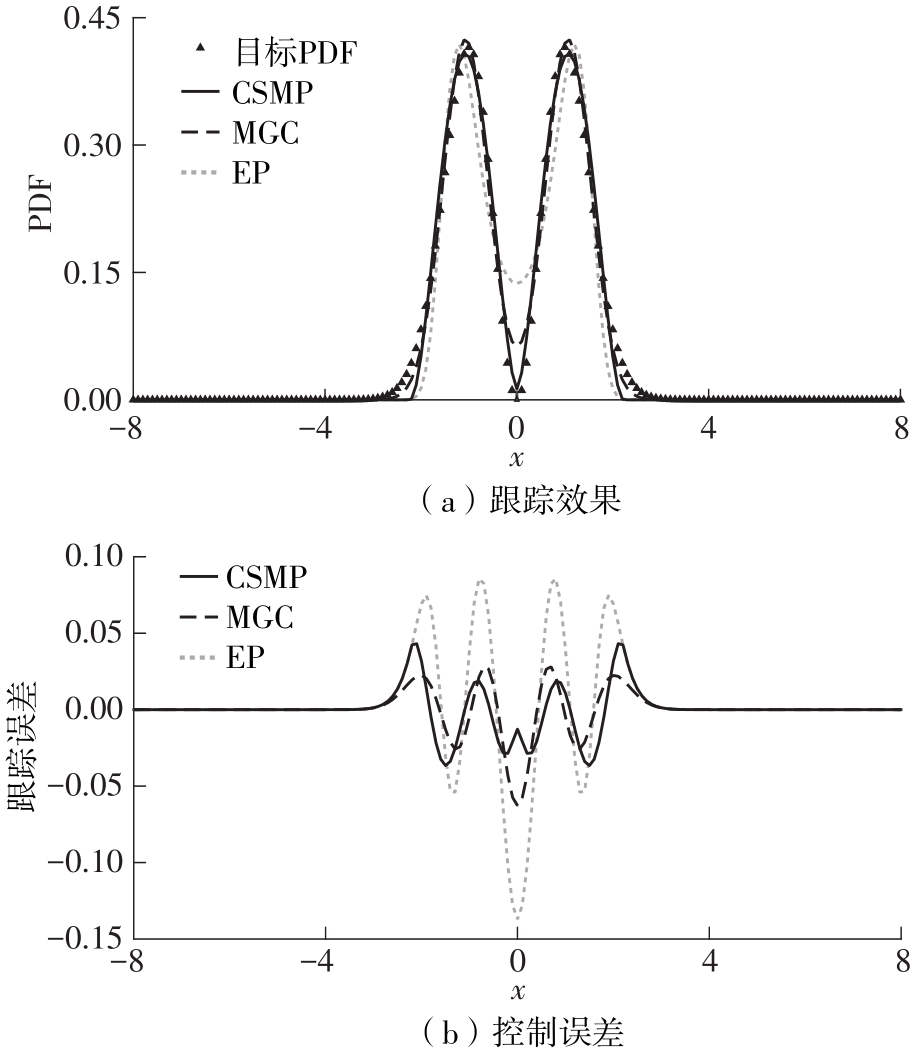
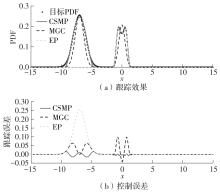
Comparison of the first four orders of moments among three methods for the statistical characteristics of one-dimensional state variable PDF"
| PDF形状 | 均值 | 方差 | 峰度 | 偏度 | |
|---|---|---|---|---|---|
| 单峰 | 目标PDF | 0 | 1.000 0 | 4.900 1 | 1.829 3 |
| MGC-PDF | 0 | 1.000 0 | 4.900 1 | 1.829 3 | |
| EP-PDF | 0 | 0.999 9 | 4.900 1 | 1.829 5 | |
| CSMP-PDF | 0 | 0.842 3 | 4.405 4 | 1.730 4 | |
| 双峰 | 目标PDF | 0 | 1.500 0 | 5.060 9 | 1.878 9 |
| MGC-PDF | -5.000 0×10-5 | 1.370 0 | 5.232 5 | 1.827 0 | |
| EP-PDF | -1.387 8×10-17 | 1.144 5 | 5.203 6 | 1.909 6 | |
| CSMP-PDF | -5.554 5×10-8 | 1.345 6 | 4.725 2 | 1.885 1 | |
| 三峰 | 目标PDF | -4.475 5 | 12.069 1 | 5.434 8 | 1.969 0 |
| MGC-PDF | -3.164 7 | 12.435 4 | 6.082 1 | 2.071 7 | |
| EP-PDF | 8.437 0×10-7 | 31.826 4 | 13.601 1 | 3.499 4 | |
| CSMP-PDF | -4.425 4 | 12.053 3 | 5.061 6 | 1.905 2 |
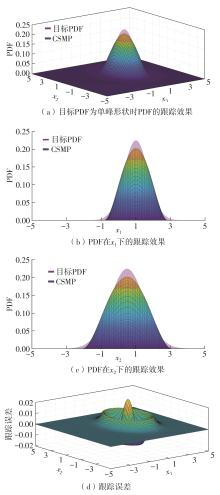
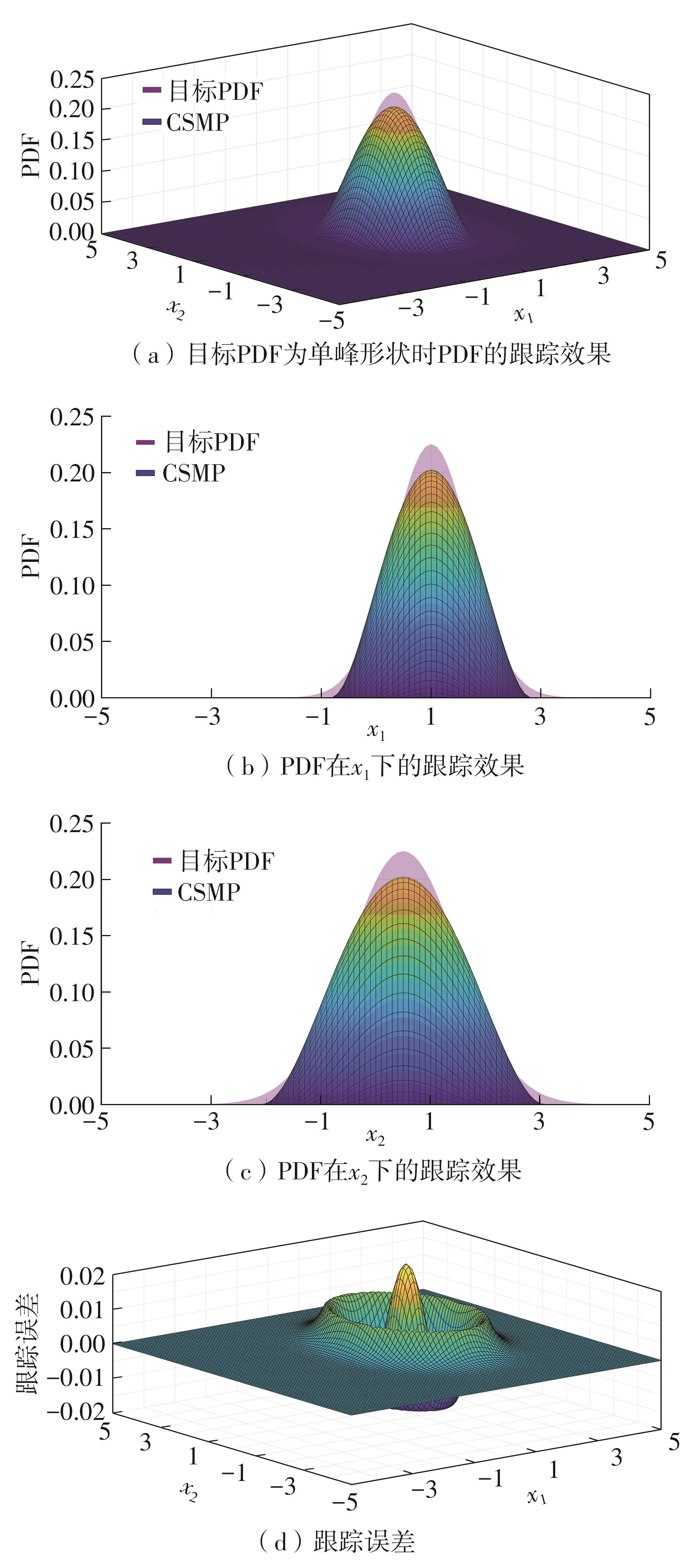
Table 3
Comparison of the first four orders of moments of the statistical characteristics of two-dimensional state variable PDF"
| 状态变量 | 前四阶矩 | 目标PDF | CSMP-PDF | 误差 |
|---|---|---|---|---|
| x1 | 均值 | 1.000 0 | 1.000 0 | 0.000 0 |
| 方差 | 0.500 0 | 0.417 5 | 0.082 5 | |
| 峰度 | 4.217 4 | 3.912 1 | 0.305 2 | |
| 偏度 | 1.642 3 | 1.581 0 | 0.061 3 | |
| x2 | 均值 | 0.500 0 | 0.500 0 | 0.000 0 |
| 方差 | 1.000 0 | 0.835 2 | 0.164 8 | |
| 峰度 | 2.722 6 | 2.468 0 | 0.244 6 | |
| 偏度 | 1.123 9 | 1.053 5 | 0.070 4 |
| 1 | KARNY M .Towards fully probabilistic control design[J].Automatica,1996,32(12):1719-1722. |
| 2 | WANG H .Robust control of the output probability density functions for multivariable stochastic systems[C]∥ Proceedings of the 37th IEEE Conference on Decision and Control.Tampa:Omni Press,1998:1305-1310. |
| 3 | WANG H .Robust control of the output probability density functions for multivariable stochastic systems with guaranteed stability[J].IEEE Transaction on Automatic Control,1999,44(11):2103-2107. |
| 4 | WANG H .Control for bounded pseudo ARMAX stochastic systems via linear B-spline approximations[C]∥ Proceedings of the 39th IEEE Conference on Decision and Control.Sydney:IEEE,2000:3369-3374. |
| 5 | WANG H, ZHANG J H .Bounded stochastic distributions control for pseudo-ARMAX stochastic systems[J].IEEE Transactions on Automatic Control,2001,46(3):486-490. |
| 6 | WANG H .Minimum entropy control of non-Gaussian dynamic stochastic systems[J].IEEE Transactions on Automatic Control,2002,47(2):398-403. |
| 7 | WANG H, SUN X B .Neural network based probability density function shape control for unknown stochastic systems[C]∥ Proceedings of the 2004 IEEE International Symposium on Intelligent Control.Taipei:IEEE,2004:120-125. |
| 8 | WANG H, ZHANG J F, YUE H .Multi-step predictive control of a PDF-shaping problem[J].Acta Automatica Sinica,2005,31(2):274-279. |
| 9 | GUO L, WANG H .PID controller design for output PDFs of stochastic systems using linear matrix inequalities[J].IEEE Transactions on Systems,Man and Cybernetics,Part B:Cybernetics,2005,35(1):65-71. |
| 10 | 吴凌尧,孙海琴,徐慧玲,等 .随机分布系统基于广义H∞控制的PDF跟踪控制[J].青岛大学学报(工程技术版),2008,23(4):1-7. |
| WU Ling-yao, SUN Hai-qin, XU Hui-ling,et al .H∞ state feedback control of the descriptor system for the output PDF tracking control of stochastic systems[J].Journal of Qingdao University (Engineering & Technology Edition),2008,23(4):1-7. | |
| 11 | 栾小丽,刘飞 .输出概率密度函数鲁棒弹性最优跟踪控制[J].控制工程,2008,15(5):493-496. |
| LUAN Xiaoli, LIU Fei .Robust resilient optimal tracking control for output probability design function[J].Control Engineering of China,2008,15(5):493-496. | |
| 12 | QIAN F C, GAO J J, LI D .Complete statistical characterization of discrete-time LQG and cumulant control[J].IEEE Transactions on Automatic Control,2012,57(8):2110-2115. |
| 13 | 戴喜生,邓飞其 .非线性积分微分随机系统的完全可控性[J].华南理工大学学报(自然科学版),2010,38(6):55-59. |
| DAI Xi-sheng, DENG Fei-qi .Complete controllability of nonlinear integrodifferential stochastic systems[J].Journal of South China University of Technology (Natural Science Edition),2010,38(6):55-59. | |
| 14 | 杜佳璐,李文华,郑凯,等 .船舶动力定位系统的非线性输出反馈控制[J].华南理工大学学报(自然科学版),2012,40(2):70-75,91. |
| DU Jia-lu, LI Wen-hua, ZHENG Kai,et al .Nonlinear output feedback control of dynamic positioning system of ships[J].Journal of South China University of Technology (Natural Science Edition),2012,40(2):70-75,91. | |
| 15 | 杨浩,裴海龙 .一类含高阶非匹配扰动项的非仿射非线性系统的跟踪控制[J].华南理工大学学报(自然科学版),2020,48(12):43-51. |
| YANG Hao, PEI Hailong .Tracking control for a class of nonaffine nonlinear systems with high-order mismatched disturbances[J].Journal of South China University of Technology (Natural Science Edition),2020,48(12):43-51. | |
| 16 | 律梦泽,陈建兵 .非平稳随机激励下高维非线性系统可靠度分析的概率密度全局演化方法[J].振动工程学报,2024,37(6):1-13. |
| Meng-ze LÜ, CHEN Jian-bing .GE‑GDEE for reliability analysis of high‑dimensional nonlinear systems enforced by non‑stationary stochastic excitations[J].Journal of Vibration Engineering,2024,37(6):1-13. | |
| 17 | JAIN A K, BHASIN S .Tracking control of uncertain nonlinear systems with unknown constant input delay[J].IEEE/CAA Journal of Automatica Sinica,2020,7(2):420-425. |
| 18 | FORBES M G, FORBES J F, GUAY M .Control design for discrete-time stochastic nonlinear processes with a nonquadratic performance objective[C]∥ Proceedings of the 42nd IEEE International Conference on Decision and Control.Maui:IEEE,2003:4243-4248. |
| 19 | FORBES M G .Performance characterization and regulatory feedback control design for time-invariant discrete-time stochastic processes[D].Edmonton:University of Alberta,2003. |
| 20 | FORBES M G, GUARY M, FORBES J F .Control design for first-order processes:shaping the probability density of the process state[J].Journal of Process Control,2004,14(4):399-410. |
| 21 | MICJAEL G F, MARTIN G, FORBES J F .Probabilistic control design for continuous-time stochastic nonlinear systems:a PDF shaping approach[C]∥ Proceedings of the 2004 IEEE International Symposium on Intelligent Control.Taipei:IEEE,2004:132-136. |
| 22 | CRESPO L G, SUN J Q .Non-linear stochastic control via stationary response design[J].Probabilistic Engineering Mechanics,2003,18(1):79-86. |
| 23 | GUO L, WANG H, WANG A P .Optimal probability density function control for NARMAX stochastic systems[J].Automatica,2008,44(7):1904-1911. |
| 24 | 朱晨烜,柳扬 .非线性随机系统的概率密度追踪控制[J].自动化学报,2012,38(2):197-205. |
| ZHU Chen-xuan, LIU Yang .Target control design for stationary probability density function of nonlinear stochastic system[J].Acta Automatica Sinica,2012,38(2):197-205. | |
| 25 | 赵彦彦,黄姣茹,秦新强,等 .一类随机非线性系统状态变量密度函数控制方法研究[J].西安理工大学学报,2013,29(2):144-148. |
| ZHAO Yanyan, HUANG Jiaoru, QIN Xinqiang,et al .The study of stochastic non-linear system state variable density function control method[J].Journal of Xi’an University of Technology,2013,29(2):144-148. | |
| 26 | 杨恒占,钱富才,高韵,等 .随机系统的概率密度函数形状调节[J].物理学报,2014,63(24):240508/1-8. |
| YANG Heng-zhan, QIAN Fu-cai, GAO Yun,et al .The shape regulation of probability density function for stochastic systems[J].Acta Physica Sinica,2014,63(24):240508/1-8. | |
| 27 | 杨恒占,钱富才,黄姣茹,等 .一类随机系统完全统计特征控制[J].控制理论与应用,2016,33(5):669-675. |
| YANG Heng-zhan, QIAN Fu-cai, HUANG Jiao-ru,et al .The complete statistical characterization control for a class of stochastic systems[J].Control Theory & Applications,2016,33(5):669-675. | |
| 28 | 杨恒占,钱富才,高嵩,等 .一类随机系统的概率密度函数形状控制[J].系统工程理论与实践,2016,36(9):2424-2431. |
| YANG Hengzhan, QIAN Fucai, GAO Song,et al .The shape control of probability density function for a class of stochastic systems[J].Systems Engineering-Theory & Practice,2016,36(9):2424-2431. | |
| 29 | 杨恒占,付月园,高嵩,等 .基于MGC法的非线性随机系统PDF控制[J].控制与决策,2019,34(7):1463-1468. |
| YANG Heng-zhan, FU Yue-yuan, GAO Song,et al .PDF control of nonlinear stochastic systems based on MGC method[J].Control and Decision,2019,34(7):1463-1468. | |
| 30 | WANG L Z, QIAN F C, LIU J .Shape control on probability density function in stochastic systems[J].Journal of Systems Engineering and Electronics,2014,25(1):144-149. |
| 31 | WANG L Z, QIAN F C, LIU J .The PDF shape control of the state variable for a class of stochastic systems[J].International Journal of Systems Science,2015,46(12):2231-2239. |
| 32 | WANG L Z, QIAN F C .Shaping the PDF of the state variable based on piecewise linear control for non-linear stochastic systems[J].Science China:Information Sciences,2016,59(11):106-116. |
| 33 | WANG L Z, QIAN F C .Technique of probability density function shape control for nonlinear stochastic systems[J].Journal of Shanghai Jiaotong University (Science),2015,20(2):129-134. |
| 34 | WANG L Z, XIE G, QIAN F C,et al .Developing an innovative method to control the probability density function shape of the state response for nonlinear stochastic systems[J].International Journal of Robust and Nonlinear Control,2021,31(16):7904-7919. |
| 35 | WANG L Z, XIE G, QIAN F C,et al .A novel PDF shape control approach for nonlinear stochastic systems[J].IEEE/CAA Journal of Automatica Sinica,2022,9(8):1490-1498. |
| 36 | 鄂国康,姚伟彬 .求大规模非线性随机动力系统概率密度函数解的子空间法[J].固体力学学报,2010,31(专辑):164-170. |
| ER G K, IU V P .Subspace method for the PDF solutions of large-scale nonlinear stochastic dynamic systems[J].Chinese Journal of Solid Mechanics,2010,31(S. Issue):164-170. | |
| 37 | 戎海武,孟光,王向东,等 .FPK方程的近似闭合解[J].应用力学学报,2003,20(3):95-98. |
| RONG Haiwu, MENG Guang, WANG Xiangdong,et al .Approximation solution of FPK equations[J].Chinese Journal of Applied Mechanics,2003,20(3):95-98. | |
| 38 | 孙鹏,刘建华,姜文安,等 .二阶FPK方程的概率密度演化分析[J].江西科学,2018,36(5):709-715. |
| SUN Peng, LIU Jianhua, JIANG Wenan,et al .Probability density evolution of second-order FPK equations[J].Jiangxi Science,2018,36(5):709-715. | |
| 39 | GUNEL S, SAVACI F A .Approximate stationary density of the nonlinear dynamical systems excited with white noise[C]∥ Proceedings of 2005 IEEE International Symposium on Circuits and Systems.Kobe:IEEE,2005:4899-4902. |
| 40 | MIRJALILI S .Moth-flame optimization algorithm:a novel nature-inspired heuristic paradigm[J].Knowledge-Based Systems,2015,89:228-249. |
| [1] | HU Xinghua, CHEN Xinghui, WANG Ran, et al. Optimization Model of Bus Priority Control Considering Carbon Emissions with Stochastic Characteristics [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(10): 160-170. |
| [2] | Ouyang Sen Shi Yi- li Pan Wei Feng Tian- rui. A New Method to Evaluate Sensitivity of Sensitive Load to Voltage Sag [J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(8): 9-14. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||