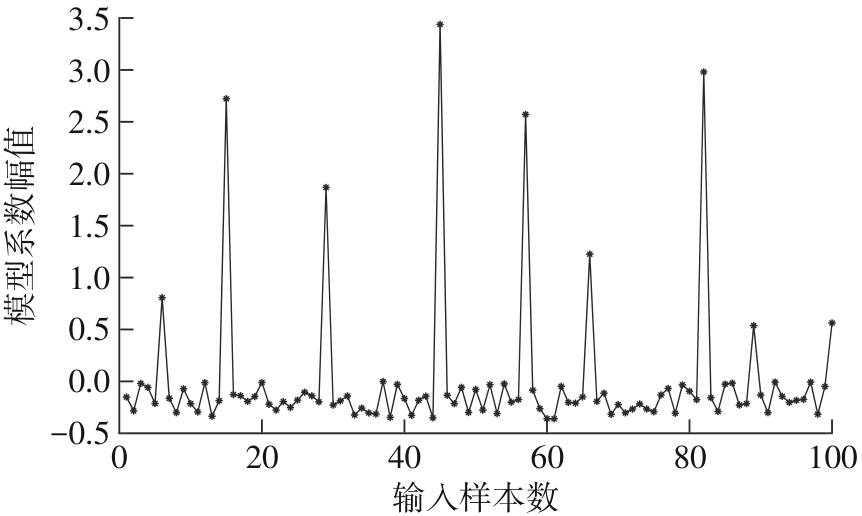
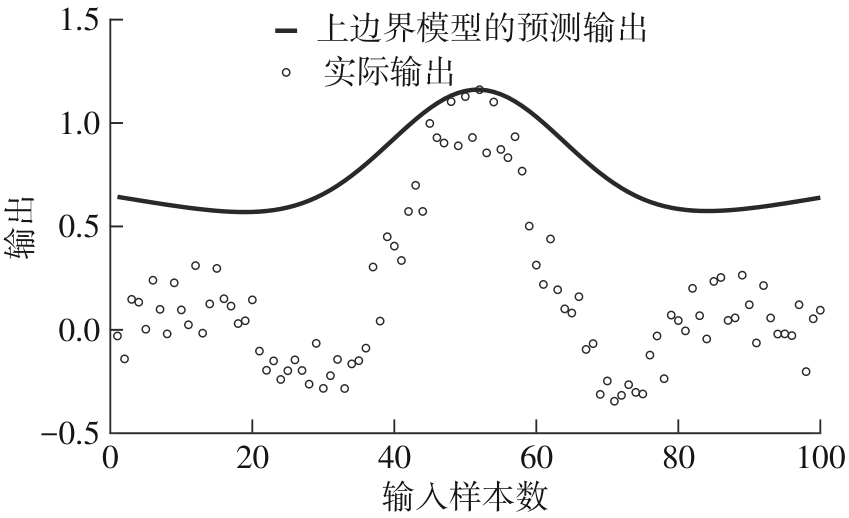
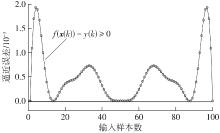
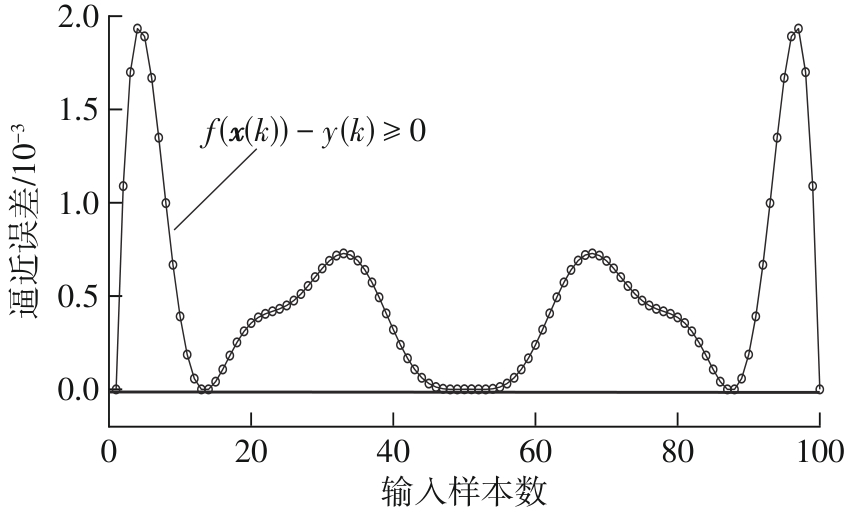
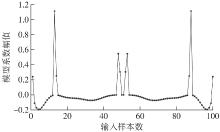
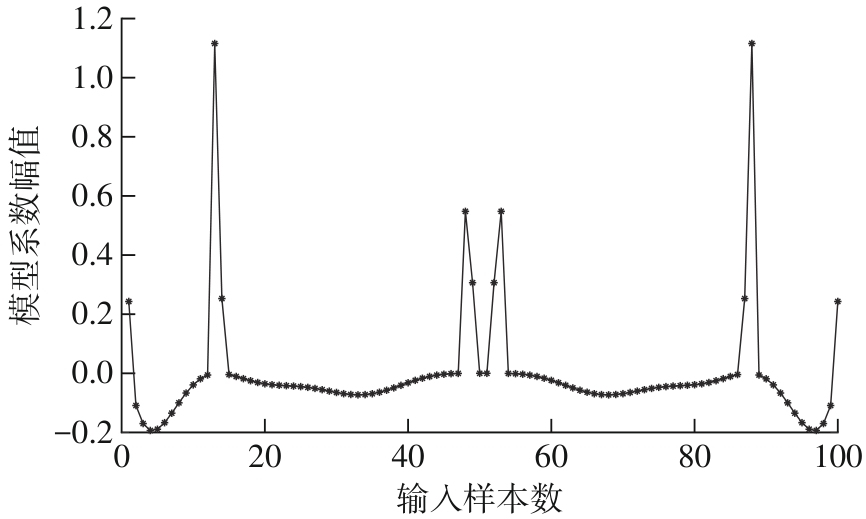
Journal of South China University of Technology(Natural Science Edition) ›› 2024, Vol. 52 ›› Issue (12): 139-150.doi: 10.12141/j.issn.1000-565X.240283
Special Issue: 2024年流体动力与机电控制工程
• Fluid Power & Mechatronic Control Engineering • Previous Articles
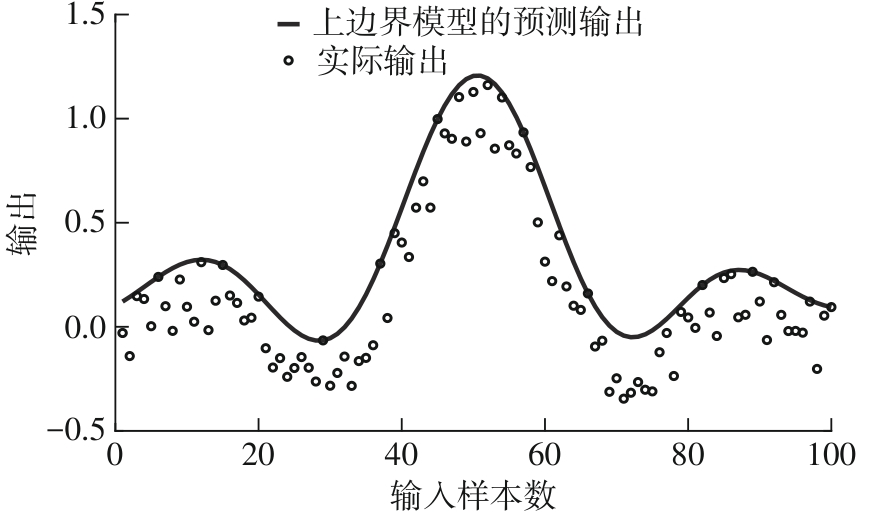
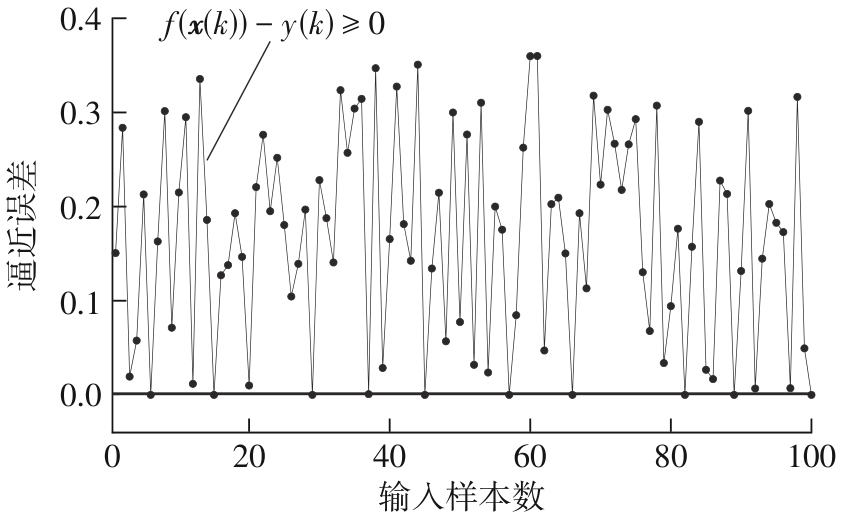
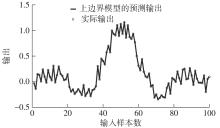
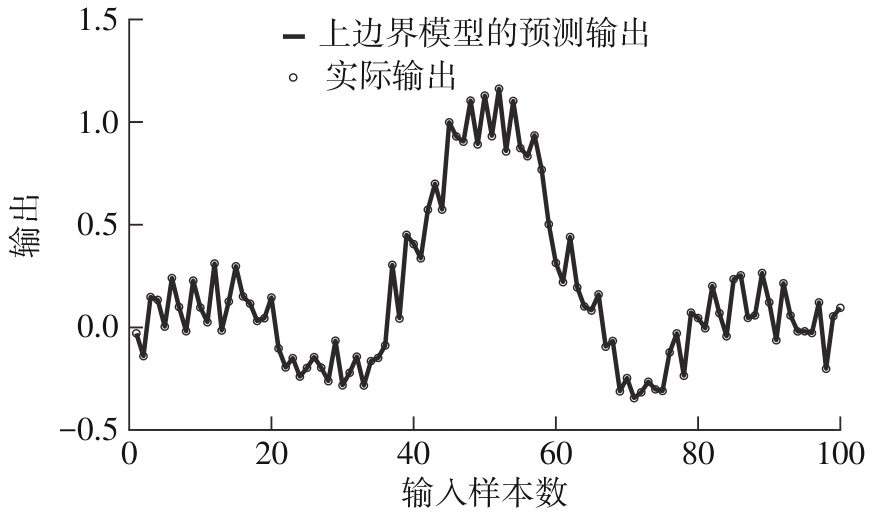
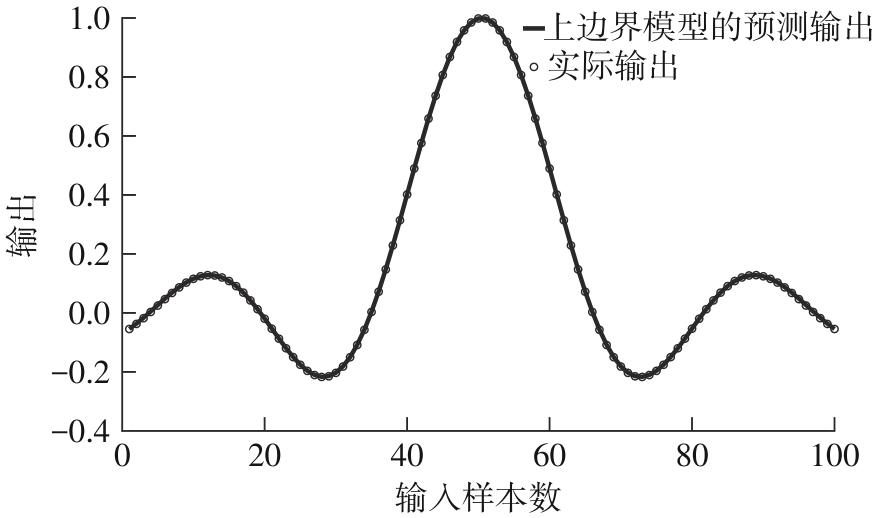
Construction of Upper Boundary Model Based on Least Squares Support Vector Regression
LIU Xiaoyong ZENG Chengbin LIU Yun HE Guofeng YAN Genglong
- Automation Department of Brewing Engineering,Moutai Institute,Renhuai 564507,Guizhou,China
-
Received:2024-06-04Online:2024-12-25Published:2024-09-27 -
Supported by:the National Natural Science Foundation of China(61966006);the Natural Science Foundation of Guizhou Province(ZK[2023]YB449)
CLC Number:
Cite this article
LIU Xiaoyong, ZENG Chengbin, LIU Yun, et al. Construction of Upper Boundary Model Based on Least Squares Support Vector Regression[J]. Journal of South China University of Technology(Natural Science Edition), 2024, 52(12): 139-150.
share this article
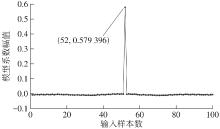
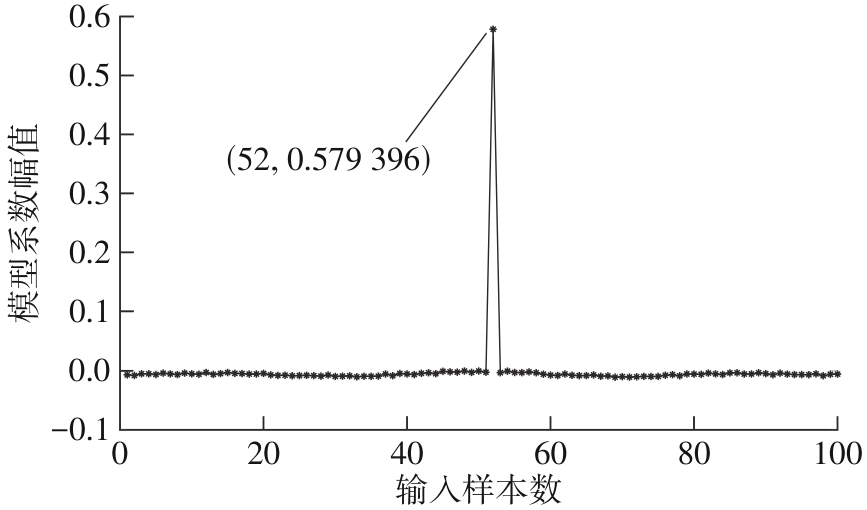
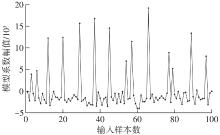
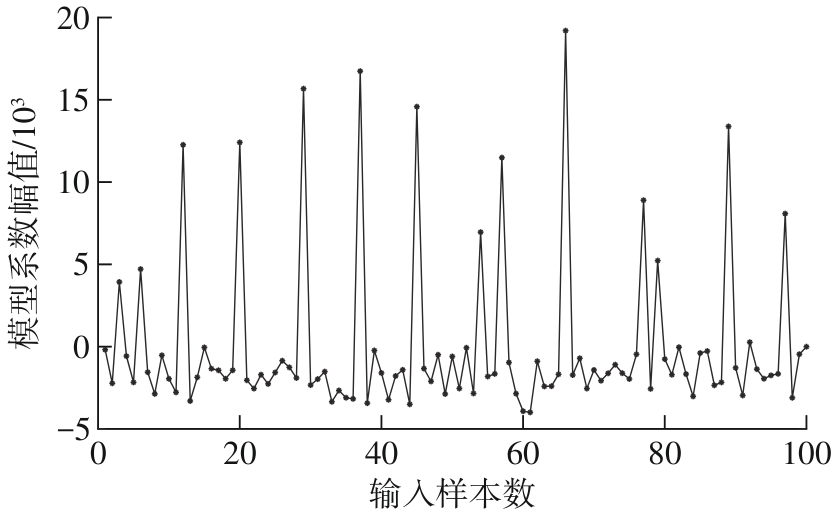
Table 1
Variations of My^, Mλ and Msparsity when σ=2.50,0.25"
| Msparsity | ||||
|---|---|---|---|---|
| 2.50 | 0.01 | 0.582 8 | 0.761 2 | 0.631 8 |
| 0.02 | 0.847 4 | 0.648 9 | 0.476 6 | |
| 0.05 | 1.228 0 | 0.561 4 | 0.365 9 | |
| 0.08 | 1.449 8 | 0.529 7 | 0.323 3 | |
| 0.10 | 1.569 0 | 0.513 5 | 0.303 7 | |
| 0.20 | 1.921 4 | 0.461 7 | 0.247 6 | |
| 0.50 | 4.072 8 | 0.414 6 | 0.205 1 | |
| 0.80 | 5.613 1 | 0.409 3 | 0.200 4 | |
| 1.00 | 6.706 2 | 0.408 8 | 0.200 0 | |
| 10.00 | 59.798 4 | 0.402 1 | 0.195 0 | |
| 20.00 | 112.810 8 | 0.400 4 | 0.193 9 | |
| 30.00 | 165.709 9 | 0.399 7 | 0.193 6 | |
| 50.00 | 271.220 5 | 0.398 6 | 0.193 0 | |
| 80.00 | 431.782 4 | 0.398 1 | 0.192 8 | |
| 100.00 | 540.263 1 | 0.397 8 | 0.192 6 | |
| 1 000.00 | 4 957.600 0 | 0.393 7 | 0.190 0 | |
| 10 000.00 | 48 357.000 0 | 0.392 2 | 0.189 2 | |
| 0.25 | 0.01 | 0.337 3 | 0.858 9 | 0.807 9 |
| 0.10 | 1.231 8 | 0.550 7 | 0.354 2 | |
| 1.00 | 2.579 7 | 0.304 0 | 0.125 9 | |
| 10.00 | 10.515 3 | 0.200 3 | 0.070 2 | |
| 100.00 | 42.456 7 | 0.125 9 | 0.029 7 | |
| 1 000.00 | 77.877 8 | 0.054 5 | 0.005 5 | |
| 10 000.00 | 85.901 0 | 0.018 1 | 0.000 6 |
Table 2
Variations of My^, Mλ and Msparsity when σ is 0.50"
| Msparsity | M | ||
|---|---|---|---|
| 0.01 | 0.227 9 | 0.541 5 | 0.390 4 |
| 0.10 | 0.538 8 | 0.279 0 | 0.127 8 |
| 1.00 | 1.053 5 | 0.149 0 | 0.074 0 |
| 5.00 | 2.487 7 | 0.110 3 | 0.069 0 |
| 10.00 | 3.791 0 | 0.102 1 | 0.069 2 |
| 15.00 | 5.394 2 | 0.098 1 | 0.068 9 |
| 20.00 | 6.438 3 | 0.094 7 | 0.068 7 |
| 25.00 | 7.788 3 | 0.092 4 | 0.068 6 |
| 100.00 | 18.883 1 | 0.074 1 | 0.068 0 |
| 1 000.00 | 100.653 5 | 0.053 3 | 0.067 6 |
| 10 000.00 | 746.371 3 | 0.046 1 | 0.067 5 |
| 1 | SHANG D Y, LI X P, YIN M,et al .Neural network model identification control of dual-inertia system with a flexible load considering payload mass variation and nonlinear deformation[J].Engineering Applications of Artificial Intelligence,2024,128:107503/1-19. |
| 2 | MENG X, ZHANG Y, QUAN L,et al .A self-organizing fuzzy neural network with hybrid learning algorithm for nonlinear system modeling[J].Information Sciences,2023,642:119145/1-20. |
| 3 | LI J, SONG G, YAN J,et al .Data-driven fault detection and classification for MTDC systems by integrating HCTSA and soft max regression[J].IEEE Transactions on Power Delivery,2022,37(2):893-904. |
| 4 | FANG X, QU J, LIU B .Overcoming limited fault data:intermittent fault detection in analog circuits via improved GAN[J].IEEE Transactions on Instrumentation and Measurement,2024,73:1-11. |
| 5 | 哀微,朱学峰 .基于单边SPSA的动态偏差数据驱动控制算法[J].华南理工大学学报(自然科学版),2012,40(9):81-86,92. |
| AI Wei, ZHU Xue-feng .One-sided SPSA-based data-driven control algorithm with dynamic deviations[J].Journal of South China University of Technology (Natural Science Edition),2012,40(9):81-86,92. | |
| 6 | 李中奇,周靓,杨辉 .高速动车组数据驱动无模型自适应积分滑模预测控制[J].自动化学报,2024,50(1):194-210. |
| LI Zhongqi, ZHOU Liang, YANG Hui .Data-driven model-free adaptive integral sliding mode predictive control for high-speed electric multiple unit[J].Acta Automatica Sinica,2024,50(1):194-210. | |
| 7 | BOUBOULIS P, THEODORIDIS S, MAVROFORAKIS C,et al .Complex support vector machines for regression and quaternary classification[J].IEEE Transactions on Neural Networks and Learning Systems,2015,26(6):1260-1274. |
| 8 | 黄伟,黄遥,牛继强,等 .基于多尺度LBP和复合核的高光谱图像分类方法[J].信阳师范学院学报(自然科学版),2021,34(2):300-307. |
| HUANG Wei, HUANG Yao, NIU Jiqiang,et al .Hyperspectral image classification based on multi-scale local binary pattern and composite kernel function[J].Journal of Xinyang Normal University(Natural Science Edition),2021,34(2):300-307. | |
| 9 | BARANYI P .How to vary the input pace of a T-S fuzzy model: a TP model transformation-based approach[J].IEEE Transactions on Fuzzy Systems,2022,30(2):345-356. |
| 10 | KALTWANG S, TODOROVIC S, PANTIC M .Doub-ly sparse relevance vector machine for continuous facial behavior estimation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2016,38(9):1748-1761. |
| 11 | WANG X, JIANG B, WU S .Multivariate relevance vector regression based degradation modeling and remaining useful life prediction[J].IEEE Transactions on Industrial Electronics,2021,69(9):9514-9523. |
| 12 | HAN H, LIN Z, QIAO J .Modeling of nonlinear systems using the self-organizing fuzzy neural network with adaptive gradient algorithm[J].Neurocomputing,2017,266(29):566-578. |
| 13 | VAPNIK V .An overview of statistical learning theory[J].IEEE Transactions on Neural Networks,1999,10(5):988-999. |
| 14 | BURGES C .A tutorial on support vector machines for pattern recognition[J].Data Mining and Knowledge Discovery,1998,2(2):121-167. |
| 15 | SUYKENS J, VAN GESTEL T, DE BRABANTER J .Least squares support vector machines[M].Singapore:World Scientific,2002. |
| 16 | SUYKENS J A K, VANDEWALLE J .Least squares support vector machine classifiers[J].Neural Processing Letter,1999,9(3):293-300. |
| 17 | GOETHALS I, PELCKMANS K, SUYKENS J .Subspace identification of Hammerstein systems using least squares support vector machines[J].IEEE Transactions on Automatic Control,2005,50(10):1509-1519. |
| 18 | BAKO L, MERCERE G, LECOEUCHE S .Recursive subspace identification of Hammerstein models based on least squares support vector machines[J].IET Control Theory & Applications,2009,3(9):1209-1216. |
| 19 | LIU X, FANG H, CHEN Z .A novel cost function based on decomposing least-square support vector machine for Takagi-Sugeno fuzzy system identification[J].IET Control Theory & Applications,2014,8(5):338-347. |
| 20 | ZHENG W, WANG C, LIU D .Combustion process modeling based on deep sparse least squares support vector regression[J].Engineering Applications of Artificial Intelligence,2024,132:107869/1-14. |
| 21 | ZHANG H, WU Q, LI F .Application of online multitask learning based on least squares support vector regression in the financial market[J].Applied Soft Computing,2022,121:108754/1-26. |
| 22 | KAMM S, SUSHMA S, TIMO M .A survey on machine learning based analysis of heterogeneous data in industrial automation[J].Computers in Industry,2023,149:103930/1-14. |
| 23 | LI H, ZHANG Z, LI T .A review on physics-informed data-driven remaining useful life prediction:challenges and opportunities[J].Mechanical Systems and Signal Processing,2024,209(1):111120/1-32. |
| 24 | 刘道华,冯宸,赵岩松,等 .多尺度特征融合网络的磁共振快速重建方法[J].信阳师范学院学报(自然科学版),2023,36(1):127-131. |
| LIU Daohua, FENG Chen, ZHAO Yansong,et al .A fast MRI reconstruction method based on multi-scale feature fusion network[J].Journal of Xinyang Normal University (Natural Science Edition),2023,36(1):127-131. | |
| 25 | LI S, FANG H, LIU X .Parameter optimization of support vector regression based on sine cosine algorithm[J].Expert Systems with Applications,2018,91:63-77. |
| 26 | TIPPING M .Sparse Bayesian learning and the re-levance vector machine[J].Journal of Machine Learning Research,2001,1(3):211-244. |
| [1] | SHI Kairong PAN Wenzhi JIANG Zhengrong LUO Bin. Novel Mechanisms of Structural Optimization Based on Plant Growth Simulation Algorithm [J]. Journal of South China University of Technology(Natural Science Edition), 2019, 47(7): 40-48,57. |
| [2] | Liu Ming-bo Gao Qiang Lin Shun-jiang Chao Zhu. Secondary Voltage Emergency Control Considering Transient Voltage Stability [J]. Journal of South China University of Technology (Natural Science Edition), 2011, 39(8): 133-139,150. |
| [3] | You Guo-qiang Duan Bao-yan Zheng Fei. Multi-Objective Optimized Design of Deployable Antenna with Frequency Constraint [J]. Journal of South China University of Technology (Natural Science Edition), 2008, 36(8): 64-68. |
| [4] | Li Guo-chao Jian Qi-fei Liu Hai-yan. Application of Nonlinear Constraints to Optimized Design of Cylinder Diameter and Piston Stroke in Diesel Engines [J]. Journal of South China University of Technology (Natural Science Edition), 2005, 33(11): 107-110. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||