A 5D Multi-Stable System with Wide Range of Hyperchaotic States

doi:10.12141/j.issn.1000-565X.220620

Abstract

Abstract:

Large-scale chaotic systems are often used in secure communication and other fields, because they can provide a wider chaotic interval. Most of the existing large-scale chaotic systems are three-dimensional and four-dimensional systems. In order to obtain more chaotic and more complex systems, this study proposed a five-dimensional system with a large range of hyperchaotic states and multiple coexisting attractors. The dynamic characteristics of the five-dimensional system were analyzed by means of coexistence bifurcation diagram, coexistence phase diagram, Lyapunov exponent spectrum and calculation of system divergence. The results show that: the system is a dissipative hyperchaotic system; when the parameters are fixed, the system can produce multiple coexisting attractors only by changing the initial value, and when the parameter d takes different values, the system will produce 12 types of coexistence phenomena, which are period-1 attractor, period-2 attractor, period-4 attractor, quasi-periodic attractor, one-scroll attractor, double-scroll attractor and so on; when the parameter m varies in the range of [0.1, 4 000], the system will always maintain a hyperchaotic state, and when m is in the range of [70, 4 000], the Lyapunov exponent spectrum of the system remains unchanged and maintains a hyperchaotic state with three positive Lyapunov exponents, indicating that the system has an invariant Lyapunov exponent characteristic. FPGA (field programmable gate array) was used to realize the digital circuit, and the experimental results were observed on the oscilloscope, which verified the feasibility of the hyperchaotic system.

Key words: large-scale hyperchaotic system, positive Lyapunov exponent, coexisting attractor, field programmable gate array

CLC Number:

O415.5

ZENG Yicheng, LI Wenxuan, SUN Xiaoli. A 5D Multi-Stable System with Wide Range of Hyperchaotic States[J]. Journal of South China University of Technology(Natural Science Edition), 2024, 52(1): 139-146.

Figures/Tables 8

Fig.1

Fig.2

Fig.3

Fig.4

Fig.5

Fig.6

Fig.7

Fig.8

References 23

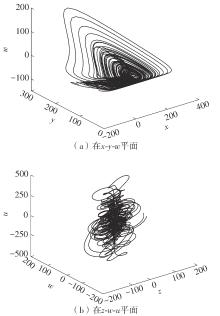
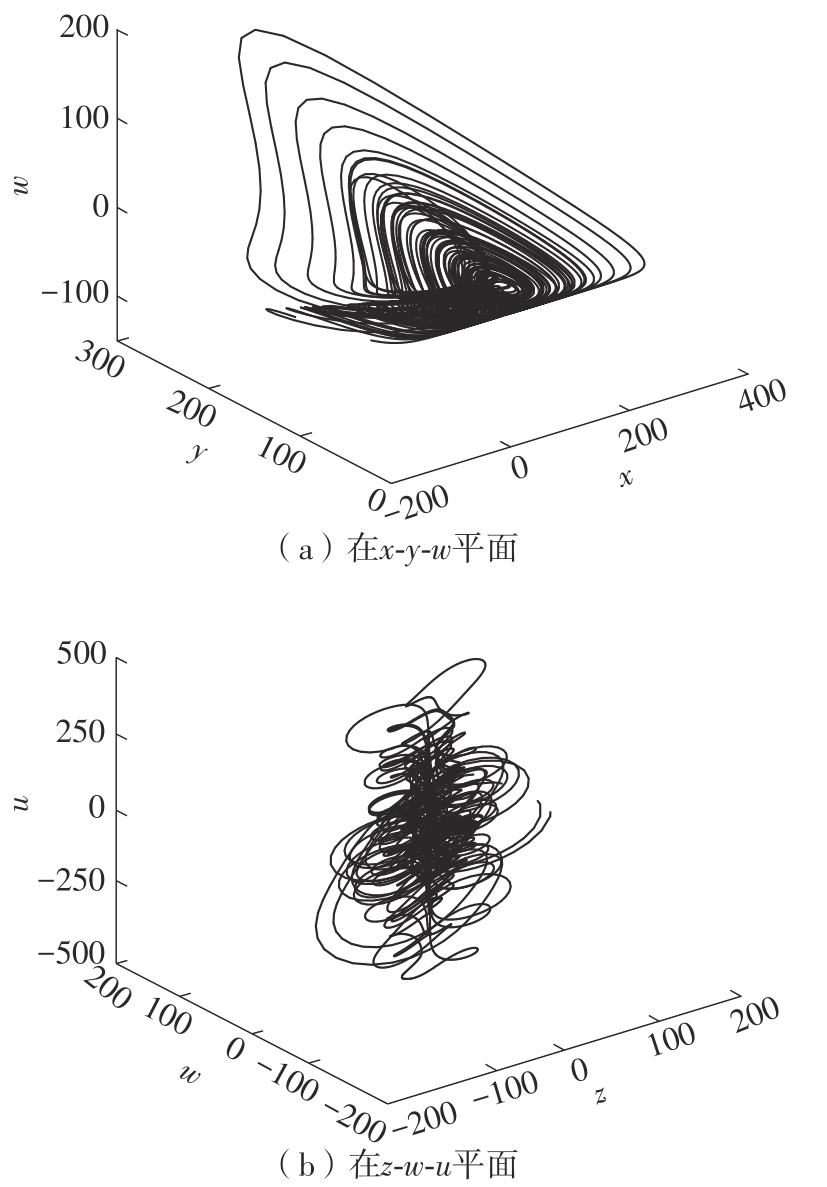
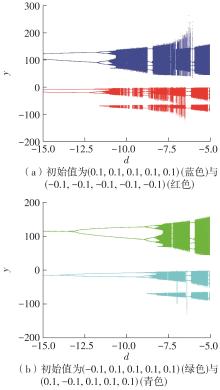
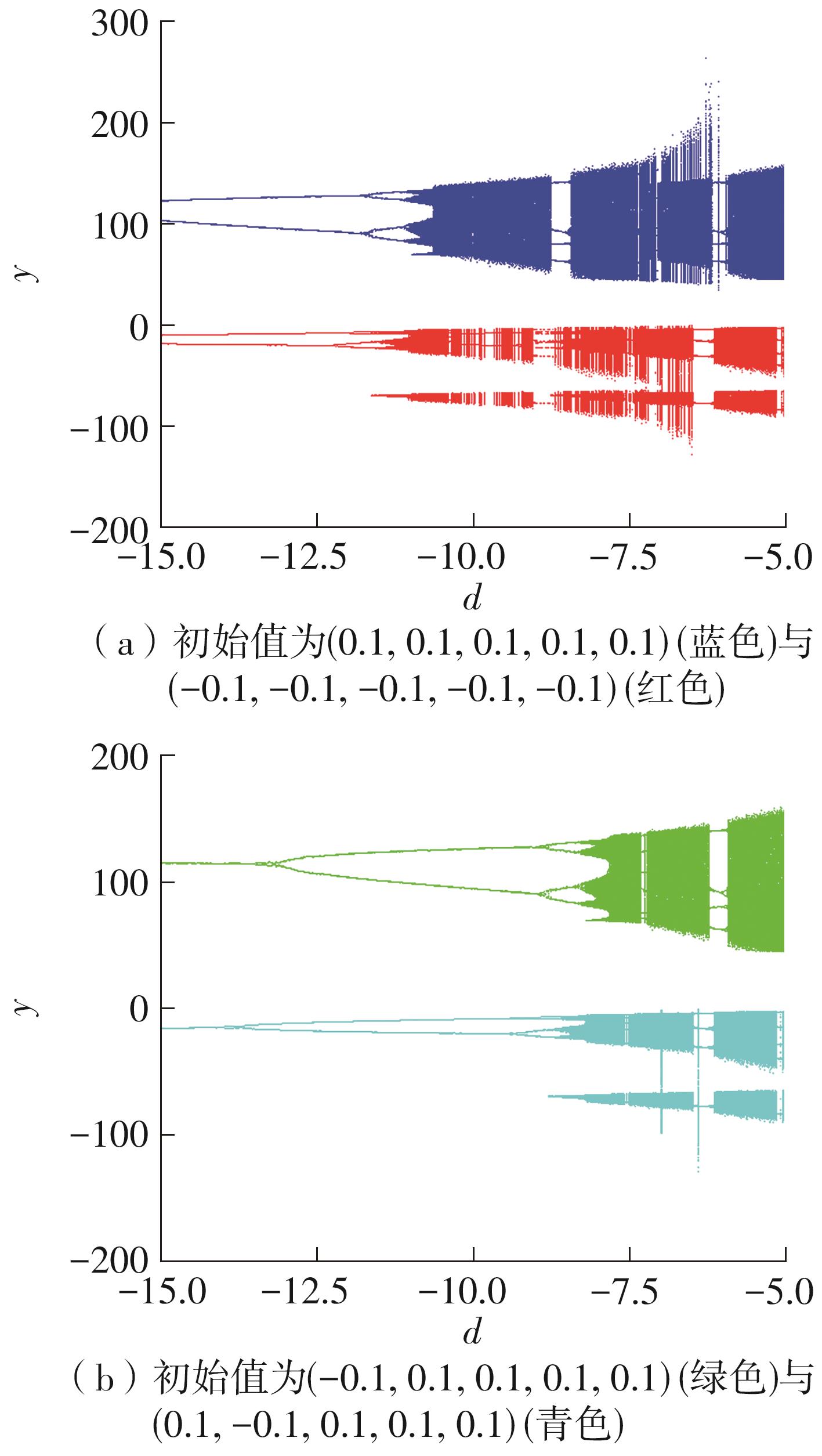
1	ZHANG Z R， CHEN P， LI W J，et al ．Design and ARM-based implementation of bitstream-oriented chaotic encryption scheme for H．264/AVC video［J］．Entropy，2021，23（11）：1431.
2	LAI Q， NOROUZI B， LIU F ．Dynamic analysis，circuit realization，control design and image encryption application of an extended Lü system with coexisting attractors［J］．Chaos，Solitons & Fractals，2018，114：230-245.
3	PENG X N， ZENG Y C ．Image encryption application in a system for compounding self-excited and hidden attractors［J］．Chaos，Solitons & Fractals，2020，139：110044/1-15.
4	BAO B C， BAO H， WANG N，et al ．Hidden extreme multistability in memristive hyperchaotic system［J］．Chaos，Solitons & Fractals，2017，94：102-111.
5	MEZATIO B A， MOTCHONGOM M T， TEKAM B R W，et al ．A novel memristive 6D hyperchaotic autonomous system with hidden extreme multistability［J］．Chaos，Solitons & Fractals，2019，120：100-115.
6	ZHANG S， ZENG Y C， LI Z J，et al ．Hidden extreme multistability，antimonotonicity and offset boosting control in a novel fractional-order hyperchaotic system without equilibrium［J］．International Journal of Bifurcation and Chaos，2018，28（13）：1850167/1-18.
7	PHAM V T， VAIDYANATHAN S， VOLOS C，et al ．A no-equilibrium hyperchaotic system with a cubic nonlinear term［J］．Optik，2016，127（6）：3259-3265.
8	万求真，陈思邈，黎婷，等．具有恒Lyapunov指数谱的新鲁棒混沌系统及电路实验［J］．湖南师范大学自然科学学报，2020，43（5）：75-82.
	WAN Qiuzhen， CHEN Simiao， LI Ting，et al ．A novel robust chaotic system with invariable Lyapunov exponent spectrum and its circuit implementation［J］．Journal of Natural Science of Hunan Normal University，2020，43（5）：75-82.
9	LI C L， LI H M， TONG Y N ．Analysis of a novel three-dimensional chaotic system［J］．Optik，2013，124（13）：1516-1522.
10	QI G Y， CHEN G R， ZHANG Y H ．On a new asymmetric chaotic system［J］．Chaos，Solitons & Fractals，2008，37（2）：409-423.
11	LIU J M， ZHANG W ．A new three-dimensional chaotic system with wide range of parameters［J］．Optik，2013，124（22）：5528-5532.
12	张泽峰，黄丽莲，项建弘，等．新的具有宽参数范围的五维保守超混沌系统的动力学研究［J］．物理学报，2021，70（23）：128-138.
	ZHANG Zefeng， HUANG Lilian， XIANG Jianhong，et al ．Dynamic study of a new five-dimensional conservative hyperchaotic system with wide parameter range［J］．Acta Physica Sinica，2021，70（23）：128-138.
13	贾红艳，陈增强，袁著祉．一个大范围超混沌系统的生成和电路实现［J］．物理学报，2009，58（7）：4469-4476.
	JIA Hongyan， CHEN Zengqiang， YUAN Zhuzhi ．Generation and circuit implementation of a large range hyper-chaotic system［J］．Acta Physica Sinica，2009，58（7）：4469-4476.
14	梅蓉，陈谋．一类超大范围超混沌系统的动力学分析和电路实现［J］．四川大学学报（工程科学版），2012，44（5）：168-172.
	MEI Rong， CHEN Mou ．Dynamic analysis of a class of large range of hyper-chaotic systems and its circuit achievement［J］．Journal of Sichuan University（Engineering Science Edition），2012，44（5）：168-172.
15	XIAN Y J， XIA C， GUO T T，et al ．Dynamical analysis and FPGA implementation of a large range chaotic system with coexisting attractors［J］．Results in Physics，2018，11：368-376.
16	徐昌彪，黎周．具有共存混沌吸引子的超大范围参数混沌系统［J］．浙江大学学报（工学版），2019，53（8）：1552-1562.
	XU Changbiao， LI Zhou ．A super-wide-range parameter chaotic system with coexisting chaotic attractor［J］．Journal of Zhejiang University （Engineering Science），2019，53（8）：1552-1562.
17	LAI B C， HE J J ．Dynamic analysis，circuit implementation and passive control of a novel four-dimensional chaotic system with multiscroll attractor and multiple coexisting attractors［J］．Pramana，2018，90（3）：1-12.
18	ZHANG S， ZENG Y C， LI Z J，et al ．Generating one to four-wing hidden attractors in a novel 4D no-equilibrium chaotic system with extreme multistability［J］．Chaos，2018，28（1）：013113/1-11.
19	鲜永菊，莫运辉，徐昌彪，等．具有多种吸引子共存类型的新型四维混沌系统［J］．华南理工大学学报（自然科学版），2020，48（3）：32-43.
	XIAN Yongju， MO Yunhui， XU Changbiao，et al ．New four-dimensional chaotic system with multiple types of coexistence of attractor［J］．Journal of South China University of Technology（Natural Science Edition），2020，48（3）：32-43.
20	WOLF A， SWIFT J B， SWINNEY H L，et al ．Determining Lyapunov exponents from a time series［J］．Physica D：Nonlinear Phenomena，1985，16（3）：285-317.
21	YANG Q G， BAI M L ．A new 5D hyperchaotic system based on modified generalized Lorenz system［J］．Nonlinear Dynamics，2017，88（1）：189-221.
22	ZHANG F C， CHEN R， WANG X Y，et al ．Dynamics of a new 5D hyperchaotic system of Lorenz type［J］．International Journal of Bifurcation and Chaos，2018，28（3）：1850036/1-12.
23	ZHANG Y G， ZENG Y C， GAO J L ．Numerical study and FPGA implementation of a new 3D chaotic system［J］．Brazilian Journal of Physics，2021，51（6）：1884-1896.

[1]	LIN Zhijian, DING Yongqiang, YANG Xiuzhi, et al. Parallel Pipeline Hardware Design of Intra Rate-Distortion Optimization Prediction Mode in HEVC [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(5): 95-103.
[2]	XIAN Yongju, MO Yunhui, XU Changbiao, et al. New Four-Dimensional Chaotic System with Multiple Types of Coexistence of Attractor [J]. Journal of South China University of Technology (Natural Science Edition), 2020, 48(3): 32-43.
[3]	TANG Wen-ming LIU Gui-xiong. FPGA Fixed-Point Technology of Exponential Function Achieved by CORDIC Algorithm [J]. Journal of South China University of Technology (Natural Science Edition), 2016, 44(7): 9-14.
[4]	Liu Gui- zhai Yu Fang Liu Zhong- li Diao Lan- song. Implementation of Priority Resource Sharing in RTL Synthesis [J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(6): 23-27.
[5]	Zhang Feng Wang Zuo-jian Wu Yang Yu Fang Liu Zhong-li. Boolean Matching of Wide Functions and Its Application to Resynthesis of FPGA [J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(5): 34-42.
[6]	Li Ming Li Yan Chen Liang Yu Fang Liu Zhong-li. Implementation of Placement and Routing Improvement for Island-Style FPGA Chips [J]. Journal of South China University of Technology(Natural Science Edition), 2012, 40(6): 16-21.
[7]	Zhu Xiao-ping Han Ye-qiang Hao Yao-yao Wang Dong Chen Yao-wu. Real-Time Sorting Algorithm of Spike Potentials Based on Probabilistic Neural Network [J]. Journal of South China University of Technology(Natural Science Edition), 2012, 40(6): 48-55.
[8]	Zhu Xiao-ping Wang Dong Chen Yao-wu. Parallel Detection Method of Neuronal Spikes Based on Lifting Wavelet [J]. Journal of South China University of Technology (Natural Science Edition), 2011, 39(10): 19-25,31.
[9]	He De-biao Chen Jian-hua Hu Jin. Design and Implementation of High-Speed Coprocessor for Elliptic Curve Cryptography [J]. Journal of South China University of Technology (Natural Science Edition), 2010, 38(5): 90-94.
[10]	Zhang Guo-long Xu Xiao-su . Implementation of High-Speed Communication Chain for Embedded Integrated Navigation System [J]. Journal of South China University of Technology (Natural Science Edition), 2009, 37(9): 77-81.
[11]	Yang Bo Yin Jun-xun Shi Lei. A RS Decoder for IP Block Error Correction and Its Implementation on FPGA [J]. Journal of South China University of Technology(Natural Science Edition), 2004, 32(11): 66-69.