Multi-Objective Optimization Based on Improved Distribution of Solutions

doi:10.12141/j.issn.1000-565X.220668

Abstract

Abstract:

For low-dimensional multi-objective optimization problems, the existing multi-objective optimization algorithms have been able to ensure the proximity to the optimal front of the problem, and balance the convergence and the diversity of solution sets. However, the uniformity of the solution is ignored in most algorithms. In the multi-objective optimization problem with irregular Pareto front, the more uniform the distribution of solution is, the more the solution can reflect the true distribution of the optimal front of the problem, and the more reasonable the choices provided to decision makers. To improve the uniform distribution of solutions, a new multi-objective optimization algorithm CM-SPEA2 is proposed based on SPEA2 algorithm and the improved individual fitness calculation. In this algorithm, firstly, the initial population is divided into different clusters by means of hierarchical clustering. Next, the original calculation method of messy degree is improved to measure the messy degree of individuals in their clusters, and the individuals with the lowest messy degree are selected as reference points. Then, based on the Manhattan distance between other individuals and the reference point, the operator representing distribution is calculated and the fitness function is improved. Finally, the fitness threshold is set to screen non-dominated individuals near the reference point, so as to indirectly adjust the environmental selection strategy, make the distribution of retained individuals more uniform, thus improving the convergence and diversity. As compared with some similar multi-objective optimization algorithms, the proposed CM-SPEA2 algorithm has certain advantages in solving IMOP, ZDT and VNT test problems.

Key words: multi-objective optimization, messy degree, SPEA2 algorithm, hierarchical clustering

CLC Number:

TP301

WANG Xuewu, FANG Junyu, GAO Jin, et al. Multi-Objective Optimization Based on Improved Distribution of Solutions[J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(8): 137-148.

Figures/Tables 12

Fig.1

Fig.2

Fig.3

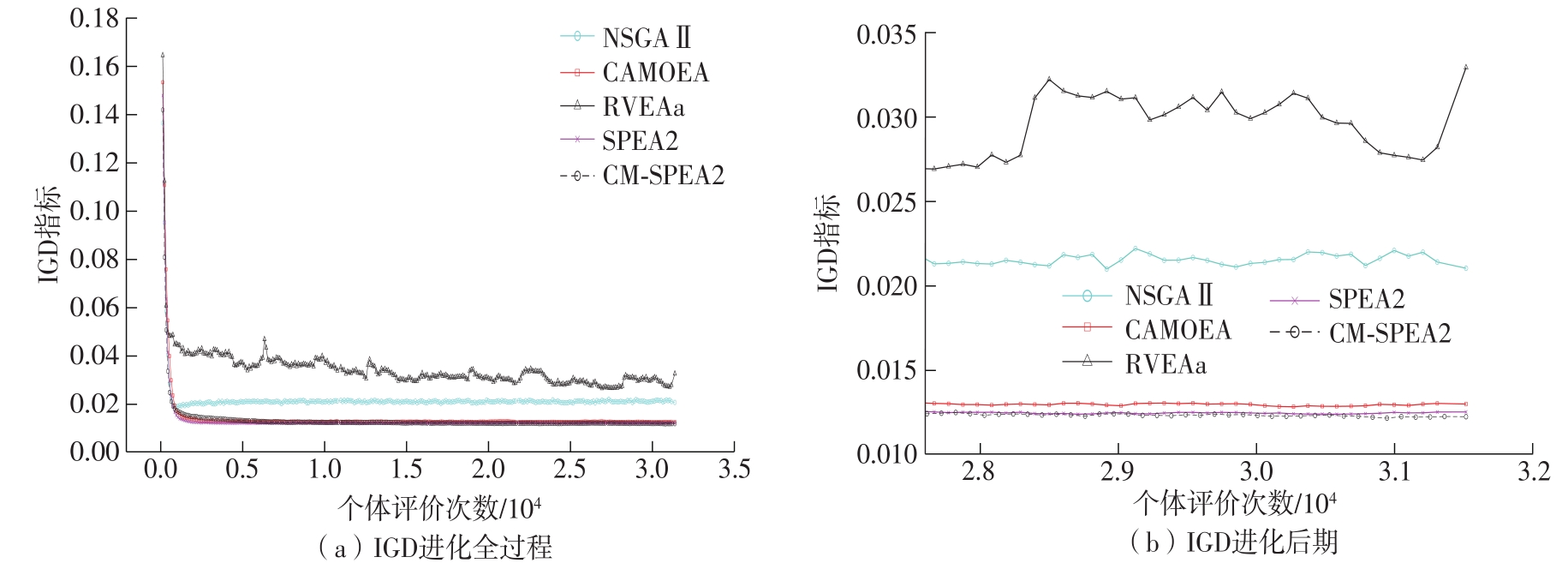
Table 1

Comparison of IGD of different algorithms in multiple MOPs"

测试问题

目标数

数值类型

不同算法的IGD指标

CM-SPEA2

SPEA2

NSGAⅡ

CAMOEA

RVEAa

IMOP1

均值

标准差

6.374 5×10^-3

1.02×10^-3

5.109 4×10^-3

3.14×10^-4+

5.919 8×10^-3

3.17×10^-4=

5.976 2×10^-3

6.61×10^-4=

1.005 5×10^-1

8.51×10^-3‒

IMOP2

均值

标准差

4.708 4×10^-3

2.18×10^-4

4.464 6×10^-3

5.24×10^-5+

5.177 6×10^-3

2.56×10^-4‒

5.177 6×10^-3

2.56×10^-4‒

5.698 0×10^-3

2.98×10^-3‒

IMOP3

均值

标准差

3.365 8×10^-3

3.77×10^-5

3.504 2×10^-3

5.06×10^-5‒

3.993 2×10^-3

1.07×10^-4‒

3.659 2×10^-3

8.54×10^-5‒

2.753 7×10^-2

5.20×10^-2‒

IMOP4

均值

标准差

6.677 1×10^-3

7.41×10^-5

6.945 9×10^-3

1.63×10^-4‒

8.665 5×10^-3

4.65×10^-4‒

7.618 3×10^-3

2.01×10^-4‒

1.392 5×10^-2

2.07×10^-3‒

IMOP5

均值

标准差

3.245 7×10^-2

4.41×10^-4

3.286 0×10^-2

5.09×10^-4‒

4.620 5×10^-2

2.97×10^-3‒

3.391 9×10^-2

8.73×10^-4‒

3.370 4×10^-2

1.09×10^-3‒

IMOP6

均值

标准差

1.163 8×10^-1

1.97×10^-1

1.165 5×10^-1

1.97×10^-1=

5.082 1×10^-2

5.27×10^-3+

3.150 0×10^-2

5.85×10^-4+

9.782 5×10^-2

1.56×10^-1+

IMOP7

均值

标准差

3.638 3×10^-2

6.28×10^-4

5.552 1×10^-2

1.10×10^-1‒

4.696 9×10^-2

3.32×10^-3‒

3.716 1×10^-2

9.84×10^-4‒

1.137 6×10^-1

2.01×10^-1=

IMOP8

均值

标准差

1.264 1×10^-1

1.48×10^-1

1.108 6×10^-1

1.14×10^-1+

1.069 4×10^-1

5.24×10^-3+

8.541 8×10^-2

3.68×10^-3+

1.528 0×10^-1

1.73×10^-1‒

ZDT1

均值

标准差

3.626 7×10^-3

3.63×10^-5

3.789 8×10^-3

6.41×10^-5‒

4.544 8×10^-3

1.39×10^-4‒

4.268 9×10^-3

9.29×10^-5‒

4.152 7×10^-3

1.64×10^-4‒

ZDT2

均值

标准差

3.724 6×10^-3

3.40×10^-5

3.741 2×10^-3

4.25×10^-5=

4.601 9×10^-3

1.36×10^-4‒

4.216 3×10^-3

1.01×10^-4‒

3.866 5×10^-1

2.96×10^-1‒

ZDT3

均值

标准差

4.392 0×10^-3

6.14×10^-5

5.641 3×10^-3

5.36×10^-3‒

6.121 1×10^-3

5.34×10^-3‒

5.840 0×10^-3

5.37×10^-3‒

8.335 1×10^-3

7.52×10^-3‒

ZDT4

均值

标准差

5.219 3×10^-3

2.03×10^-3

4.429 5×10^-3

2.75×10^-4=

5.503 7×10^-3

1.05×10^-3‒

4.923 6×10^-3

7.29×10^-4=

7.398 6×10^-3

6.52×10^-3‒

ZDT6

均值

标准差

2.944 2×10^-3

5.44×10^-5

3.006 2×10^-3

8.76×10^-5‒

3.520 6×10^-3

1.13×10^-4‒

3.352 8×10^-3

9.36×10^-5‒

3.100 8×10^-3

1.32×10^-4‒

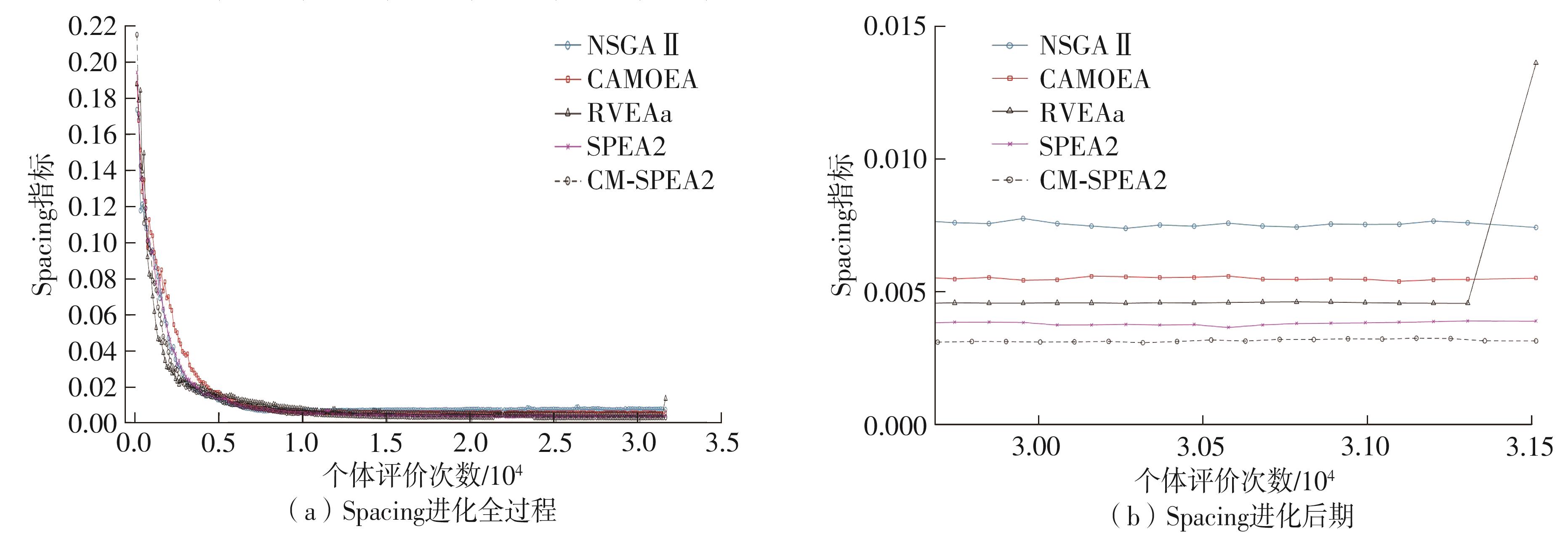
Table 1

Table 2

Table 2

Comparison of Spacing of different algorithms in multiple MOPs"

测试问题

目标数

数值类型

不同算法的Spacing指标

CM-SPEA2

SPEA2

NSGAⅡ

CAMOEA

RVEAa

IMOP1

均值

标准差

3.274 1×10^-3

5.97×10^-4

3.321 5×10^-3

2.87×10^-4=

6.458 5×10^-3

5.30×10^-4‒

4.857 6×10^-3

6.15×10^-4‒

5.087 2×10^-2

7.18×10^-3‒

IMOP2

均值

标准差

4.138 2×10^-3

1.32×10^-3

3.734 1×10^-3

4.54×10^-4=

7.021 5×10^-3

8.08×10^-4‒

6.533 4×10^-3

1.23×10^-3‒

6.438 7×10^-3

1.56×10^-3‒

IMOP3

均值

标准差

2.252 1×10^-3

2.36×10^-4

2.813 2×10^-3

3.36×10^-4‒

5.647 3×10^-3

5.21×10^-4‒

4.419 5×10^-3

4.32×10^-4‒

1.109 2×10^-2

1.80×10^-3‒

IMOP4

均值

标准差

5.790 1×10^-3

5.57×10^-4

6.918 7×10^-3

1.29×10^-3‒

1.458 8×10^-2

1.32×10^-3‒

1.083 5×10^-2

9.90×10^-4‒

1.911 6×10^-2

4.30×10^-3‒

IMOP5

均值

标准差

1.359 8×10^-2

1.53×10^-3

1.535 8×10^-2

1.66×10^-3‒

4.005 5×10^-2

3.95×10^-3‒

3.014 1×10^-2

2.05×10^-3‒

2.997 1×10^-2

3.02×10^-3‒

IMOP6

均值

标准差

1.363 0×10^-2

5.21×10^-3

1.492 4×10^-2

5.84×10^-3‒

5.177 4×10^-2

7.60×10^-3‒

3.203 4×10^-2

1.82×10^-3‒

2.993 5×10^-2

9.03×10^-3‒

IMOP7

均值

标准差

1.701 3×10^-2

2.26×10^-3

1.808 3×10^-2

3.82×10^-3‒

4.246 9×10^-2

6.53×10^-3‒

2.968 4×10^-2

2.39×10^-3‒

2.227 5×10^-2

8.51×10^-3‒

IMOP8

均值

标准差

2.809 7×10^-2

9.27×10^-3

3.555 3×10^-2

9.20×10^-3‒

8.408 6×10^-2

7.84×10^-3‒

6.620 7×10^-2

6.41×10^-3‒

5.826 1×10^-2

2.03×10^-2‒

ZDT1

均值

标准差

2.636 3×10^-3

2.74×10^-4

3.121 9×10^-3

3.12×10^-4‒

6.549 2×10^-3

5.36×10^-4‒

5.160 0×10^-3

3.90×10^-4‒

1.252 0×10^-2

1.43×10^-3‒

ZDT2

均值

标准差

2.370 1×10^-3

2.54×10^-4

3.102 7×10^-3

3.56×10^-4‒

6.869 0×10^-3

6.22×10^-4‒

5.138 2×10^-3

4.46×10^-4‒

3.536 5×10^-3

3.43×10^-4‒

ZDT3

均值

标准差

3.170 5×10^-3

4.16×10^-4

3.808 2×10^-3

4.32×10^-4‒

7.464 9×10^-3

8.15×10^-4‒

5.560 7×10^-3

5.16×10^-4‒

1.329 0×10^-2

1.36×10^-3‒

ZDT4

均值

标准差

2.504 6×10^-3

4.87×10^-4

2.728 6×10^-3

3.39×10^-4‒

6.985 7×10^-3

5.81×10^-4‒

5.100 7×10^-3

5.76×10^-4‒

1.313 3×10^-2

1.37×10^-3‒

ZDT6

均值

标准差

1.891 8×10^-3

1.80×10^-4

5.604 1×10^-3

1.85×10^-2‒

5.706 7×10^-3

5.17×10^-4‒

4.158 5×10^-3

3.99×10^-4‒

2.312 7×10^-3

2.28×10^-4‒

VNT1

均值

标准差

5.834 5×10^-2

9.33×10^-3

6.365 0×10^-2

5.72×10^-3‒

1.383 4×10^-1

1.47×10^-2‒

1.082 0×10^-1

7.05×10^-3‒

1.216 5×10^-1

1.88×10^-2‒

VNT2

均值

标准差

8.735 3×10^-3

1.12×10^-3

7.623 8×10^-3

8.57×10^-4+

1.852 2×10^-2

3.02×10^-3‒

1.202 6×10^-2

1.24×10^-3‒

5.807 9×10^-2

1.98×10^-2‒

VNT3

均值

标准差

1.942 8×10^-2

2.42×10^-3

2.138 2×10^-2

1.68×10^-3‒

6.546 6×10^-2

4.61×10^-3‒

5.745 5×10^-2

5.30×10^-3‒

8.644 2×10^-2

1.69×10^-2‒

+/‒/=数值

1/13/2

0/16/0

Table 2

Fig.4

Table 3

Fig.5

Fig.6

Fig.7

Fig.8

References 20

1	ZHANG Q， LI H ．MOEA/D：a multiobjective evolutionary algorithm based on decomposition［J］．IEEE Transactions on Evolutionary Computation，2007，11（6）：712-731．
2	ZHANG C， GAO L， LI X，et al ．Resetting weight vectors in MOEA/D for multiobjective optimization problems with discontinuous Pareto front［J］．IEEE Transactions on Cybernetics，2022，52（9）：9770-9783．
3	QI Y， LI X， YU J，et al ．User-preference based decomposition in MOEA/D without using an ideal point［J］．Swarm and Evolutionary Computation，2019，44：597-611．
4	DEB K， JAIN H ．An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach，part I：solving problems with box constraints［J］．IEEE Transactions on Evolutionary Computation，2014，18（4）：577-601．
5	DENG W， ZHANG X， ZHOU Y，et al ．An enhanced fast non-dominated solution sorting genetic algorithm for multi-objective problems［J］．Information Sciences，2022，585：441-453．
6	TIAN Y， CHENG R， ZHANG X，et al ．An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility［J］．IEEE Transactions on Evolutionary Computation，2018，22（4）：609-622．
7	TIAN Y， CHENG R， ZHANG X，et al ．A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization［J］．IEEE Transactions on Evolutionary Computation，2019，23（2）：331-345．
8	PANICHELLA A ．An adaptive evolutionary algorithm based on non-Euclidean geometry for many-objective optimization［C］∥Proceedings of the Genetic and Evolutionary Computation Conference．New York：Association for Computing Machinery，2019：595-603．
9	SONODA T， NATAKA M ．MOEA/D-S3：MOEA/D using SVM-based surrogates adjusted to subproblems for many objective optimization［C］∥Proceedings of the 2020 IEEE Congress on Evolutionary Computation （CEC）．Glasgow：IEEE，2020：1-8．
10	ZITLER M， LAUMANNS M， THIELE L ．SPEA2：improving the strength Pareto evolutionary algorithm［M］．Berlin：Springer-Verlag，2002：95-100．
11	翁理国，王安，夏旻，等．基于局部搜索的改进SPEA2算法［J］．计算机应用研究，2014，31（9）：2617-2619，2639．
	WENG Li-guo， WANG An， XIA Min，et al． Improved SPEA 2 based on local search［J］．Application Research of Computers，2014，31（9）：2617-2619，2639．
12	王学武，闵永，顾幸生．基于密度聚类的多目标粒子群优化算法［J］．华东理工大学学报（自然科学版），2019，45（3）：449-457．
	WANG Xuewu， MIN Yong， GU Xingsheng ．Multi-objective particle swarm optimization algorithm based on density clustering［J］．Journal of East China University of Science and Technology，2019，45（3）：449-457．
13	HUA Y， JIN Y， HAO K ．A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular Pareto fronts［J］．IEEE Transactions on Cybernetics，2019（7）：2758-2770．
14	李密青，郑金华，李珂．一种非均匀分布问题分布性维护方法［J］．电子学报，2011，39（4）：946-952．
	LI Mi-qing， ZHENG Jin-hua， LI Ke ．A diversity maintenance method for non-uniform distribution problem［J］．Acta Electronica Sinica，2011，39（4）：946-952．
15	郑金华，邹娟．多目标进化优化［M］．北京：科学出版社，2018：70-72．
16	TIAN Y， CHENG R， ZHANG X，et al ．PlatEMO：a MATLAB platform for evolutionary multi-objective optimization［J］．IEEE Computational Intelligence Magazine，2017，12（4）：73-87．
17	WANG H， JIAO L， YAO X ．Two_arch2：An improved two-archive algorithm for many-objective optimization［J］．IEEE Transactions on Evolutionary Computation，2015，19（4）：524-541．
18	COELLO C， CORTES N ．Solving multiobjective optimization problems using an artificial immune system［J］．Genetic Programming and Evolvable Machines，2005，6（2）：163-190．
19	SCHOTT J ．Fault tolerant design using single and multicriteria genetic algorithm optimization［D］．Cambridge：Massachusetts Institute of Technology，1995：199-200．
20	郭一楠，汤万宝，陈国玉，等．动态多目标进化优化研究进展［J］．信息与控制，2021，50（2）：162-173．
	GUO Yinan， TANG Wanbao， CHEN Guoyu，et al ．Research progress on dynamic multi-objective evolutionary optimization［J］．Information and Control，2021，50（2）：162-173．

测试问题	目标数	IGD指标		Spacing指标
测试问题	目标数	策略1	策略2	策略1	策略2
+/‒/=数值			1/2/13		2/9/5
IMOP1	2	6.334 2×10^-3	6.231 3×10^-3=	3.006 1×10^-3	3.282 4×10^-3‒
IMOP2	2	4.896 0×10^-3	4.727 7×10^-3=	4.905 4×10^-3	4.828 8×10^-1=
IMOP3	2	4.541 2×10^-3	3.369 0×10^-3+	2.215 8×10^-3	2.227 5×10^-3‒
IMOP4	3	6.704 0×10^-3	6.723 5×10^-3=	6.014 3×10^-3	6.040 2×10^-3=
IMOP5	3	3.244 5×10^-2	3.254 3×10^-2=	1.370 7×10^-2	1.385 1×10^-2‒
IMOP6	3	1.510 4×10^-1	1.685 2×10^-1=	1.239 7×10^-2	1.132 1×10^-2=
IMOP7	3	5.648 7×10^-2	7.650 2×10^-2=	1.600 7×10^-2	1.603 0×10^-2=
IMOP8	3	1.096 1×10^-1	1.400 5×10^-1=	2.744 5×10^-2	2.763 6×10^-2‒
ZDT1	2	3.622 9×10^-3	3.631 1×10^-3=	2.589 1×10^-3	2.561 9×10^-3+
ZDT2	2	3.731 9×10^-3	3.729 2×10^-3=	2.451 7×10^-3	2.500 3×10^-3‒
ZDT3	2	5.390 0×10^-3	7.345 4×10^-3‒	3.168 4×10^-3	3.798 4×10^-3
ZDT4	2	4.644 3×10^-3	4.834 7×10^-3=	2.403 1×10^-3	2.520 9×10^-3‒
ZDT6	2	2.950 7×10^-3	2.958 9×10^-3=	2.055 8×10^-3	1.960 9×10^-3=
VNT1	3	1.209 4×10^-1	1.220 6×10^-1‒	5.623 4×10^-3	6.001 8×10^-3‒
VNT2	3	1.199 2×10^-2	1.205 7×10^-2=	8.837 2×10^-3	8.652 7×10^-3+
VNT3	3	2.941 6×10^-2	2.916 4×10^-2=	1.927 2×10^-2	1.902 9×10^-2=

[1]	LI Shuxun, HU Yinggang, LI Cheng, et al. Optimization of Body Profile Line of Axial Flow Control Valve Based on Surrogate Model [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(3): 41-52.
[2]	LIU Guoyong, ZHANG Wenpeng, ZHANG Tongxin, ZHU Dongmei, ZENG Xinxi. Structural Optimization and Flow Field Characteristics of Large Format SLM Forming Bin [J]. Journal of South China University of Technology(Natural Science Edition), 2023, 51(12): 53-63.
[3]	ZHAO Kegang, HE Kunyang, LI Jie, et al. Multi-objective Energy Management Strategy of HEV Based on Improved Dynamic Programming Method [J]. Journal of South China University of Technology(Natural Science Edition), 2022, 50(9): 138-148.
[4]	JIANG Tao, LU Zhou. Multi-objective Optimization of Flat Skylights in the Elevated Railway Station [J]. Journal of South China University of Technology(Natural Science Edition), 2022, 50(7): 13-24.
[5]	LIU Hanwu, LEI Yulong, FU Yao, et al. Adaptive Regenerative Braking Control Strategy of Range-Extended Electric Vehicle Based on Multi-Objective Optimization [J]. Journal of South China University of Technology (Natural Science Edition), 2021, 49(7): 42-50,65.
[6]	JIN Xia, HU Juncong, WANG Wei, et al. Adjustment Strategy for Automobile Hood Matching in Virtual Environment [J]. Journal of South China University of Technology (Natural Science Edition), 2020, 48(6): 87-96.
[7]	DAI Xiang HUANG Xifeng TANG Rui JIANG Mengting CHEN Xingshu WANG Haizhou LUO Liang. Subtopic Detection Algorithm Based on Hierarchical Clustering [J]. Journal of South China University of Technology (Natural Science Edition), 2019, 47(8): 84-95.
[8]	WU Di LIU Li LI Xiaojun LIU Conghong. Ｒesearch on the Technologies of Passive Low Energy Buildings on the Basis of Multi-Objective Optimization Method———by Taking Cold Zone Ｒesidential Buildings for Example [J]. Journal of South China University of Technology (Natural Science Edition), 2018, 46(4): 98-104,120.
[9]	BAI Zhong-hao HE Cheng ZHU Feng. Analysis of Electromagnetic and Shock Wave Mitigation Capability of a Novel Sandwich Plate with Composites [J]. Journal of South China University of Technology (Natural Science Edition), 2016, 44(9): 137-143.
[10]	ZHAI Zhen-kun LI Di. Parameter Selection of CNC Real-Time Task on the Basis of Multi-Objective Optimization [J]. Journal of South China University of Technology (Natural Science Edition), 2016, 44(3): 23-28.
[11]	Zhou Jie Tao Ya-ping Zhang Jian-sheng Shao Chang-wei Luo Yan. Multi-Objective Optimization of Ｒoll Forgings of Coupler Yoke Based on MBC Toolbox [J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(11): 61-66.
[12]	Yang Zhao-sheng Qu Xin Lin Ci-yun Bing Qi-chun Gong Bo-wen. Traffic Signal Optimization Method Considering Low Emissions and Short Delay [J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(10): 29-34,41.
[13]	Zhang Shu-qin Xia Hong-shan Jiang Yu Zhan Xu-ren. A Constrained Multi-Objective Genetic Simulated Annealing Algorithm for Ｒunway Scheduling [J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(10): 35-41.
[14]	Wu Shan-yu Zhang Ping Li Fang. Multi-Task Scheduling Based on Particle Swarm Optimization in Cloud Manufacturing Systems [J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(1): 105-110.
[15]	Yu Li-min Xiong Hui-yuan Zong Zhi-jian Zhang Qing. Optimal Acceleration Control Strategy of Battery Electric Vehicles Based on Dynamic Programming [J]. Journal of South China University of Technology (Natural Science Edition), 2014, 42(8): 143-148.