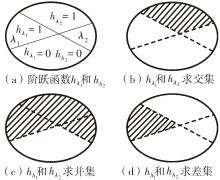
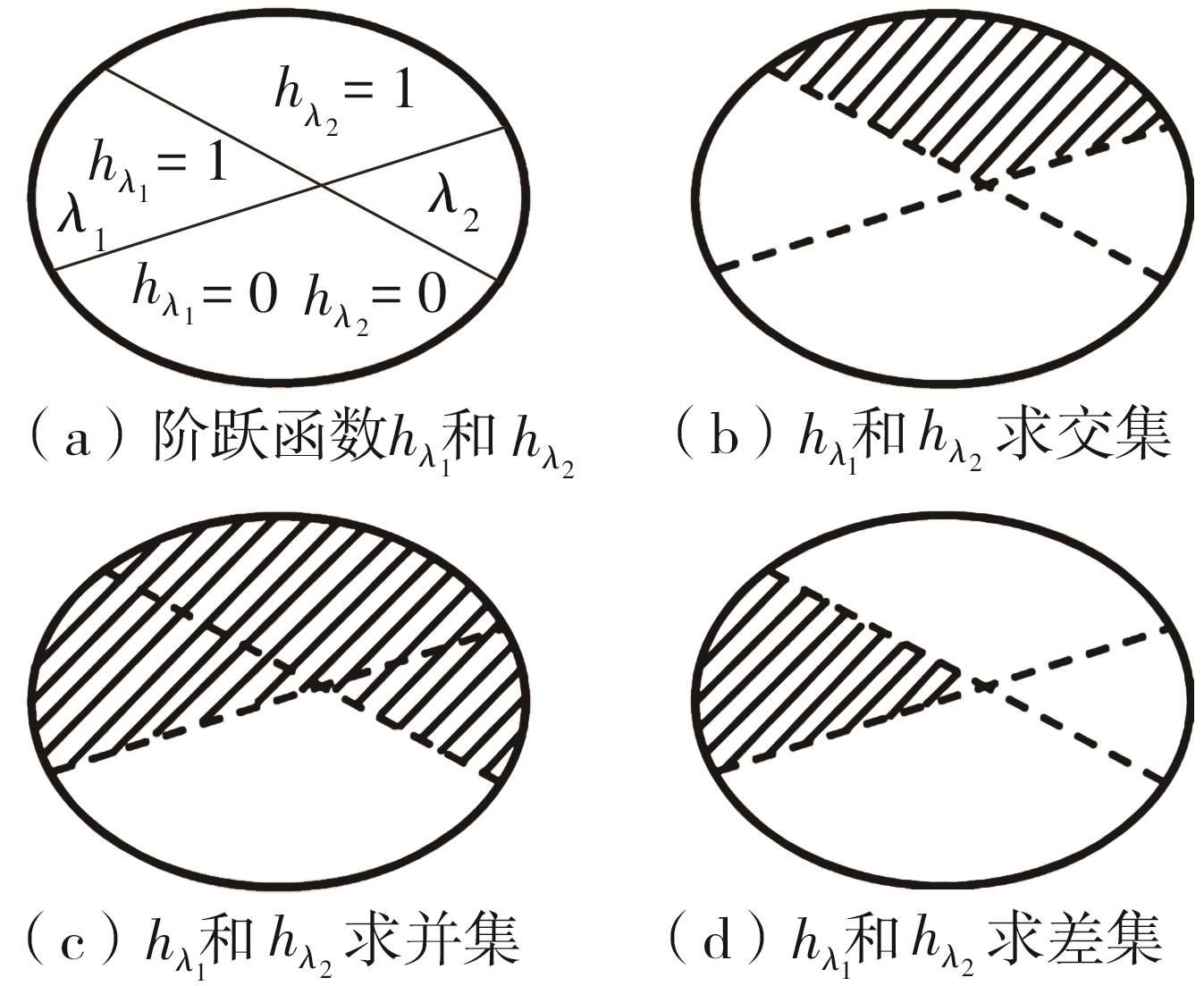
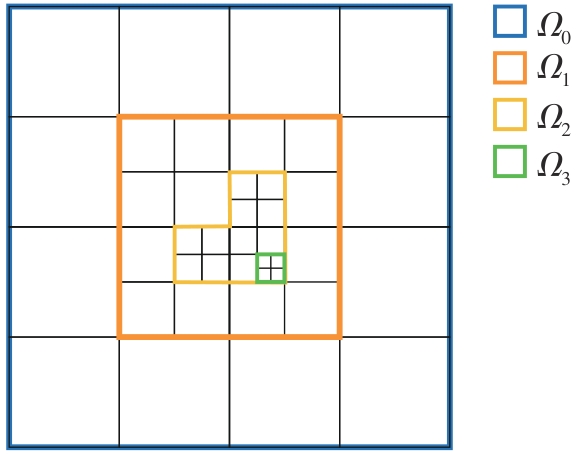
Journal of South China University of Technology(Natural Science Edition) ›› 2024, Vol. 52 ›› Issue (12): 65-78.doi: 10.12141/j.issn.1000-565X.230749
Special Issue: 2024年力学
• Mechanics • Previous Articles Next Articles
Method of Imposing Local Fixed Constraints Exactly in Isogeometric Analysis
- School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640,Guangdong,China
-
Received:2023-12-01Online:2024-12-25Published:2024-08-23 -
Supported by:the National Natural Science Foundation of China(52075184);Guangdong Basic and Applied Basic Research Foundation(2024A1515011786)
CLC Number:
Cite this article
WANG Yingjun, LI Jinghui. Method of Imposing Local Fixed Constraints Exactly in Isogeometric Analysis[J]. Journal of South China University of Technology(Natural Science Edition), 2024, 52(12): 65-78.
share this article
Table 2
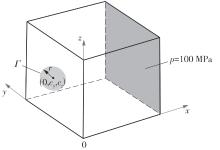
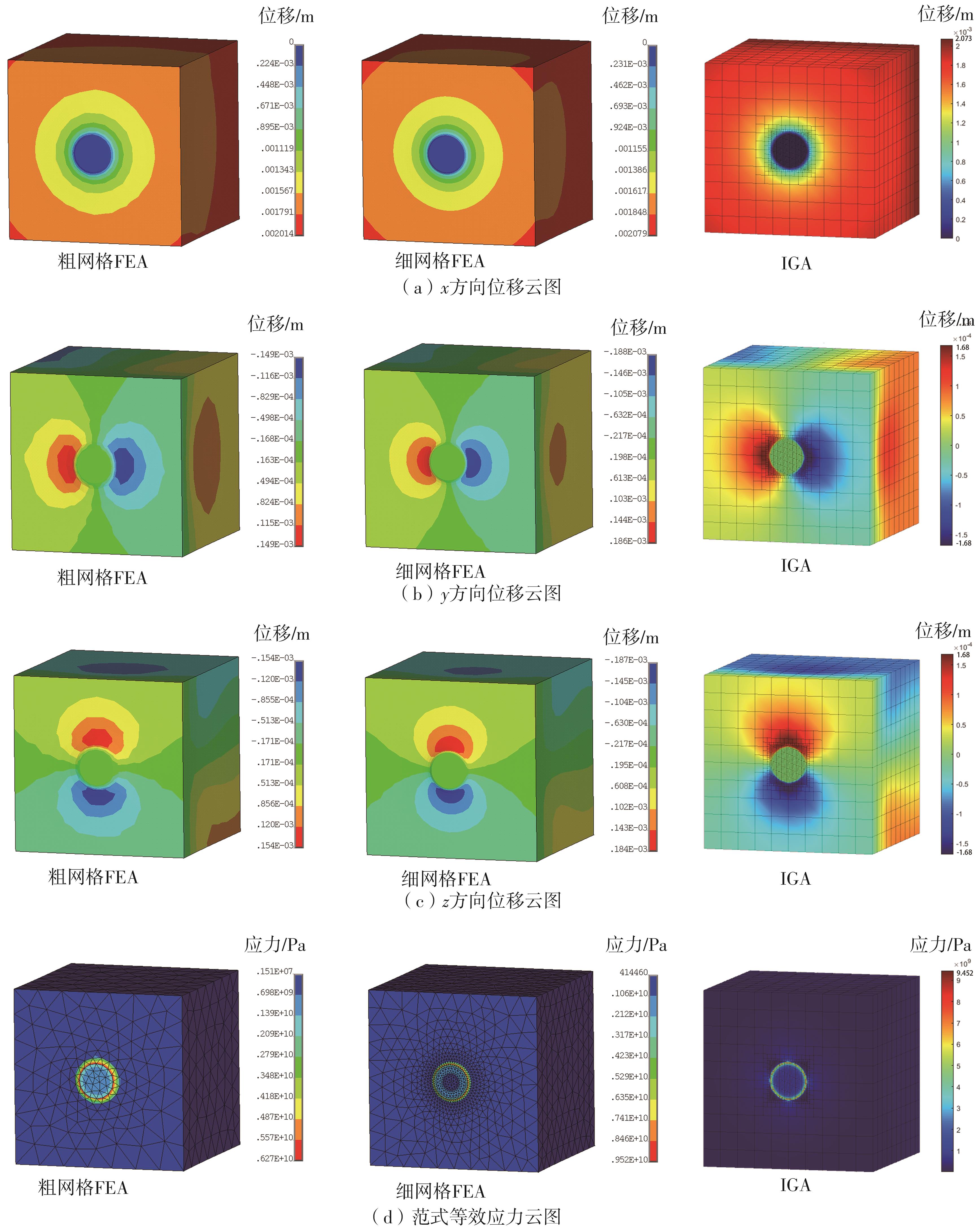
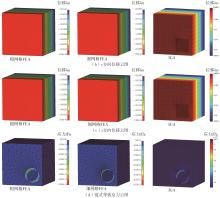
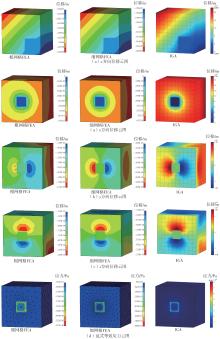
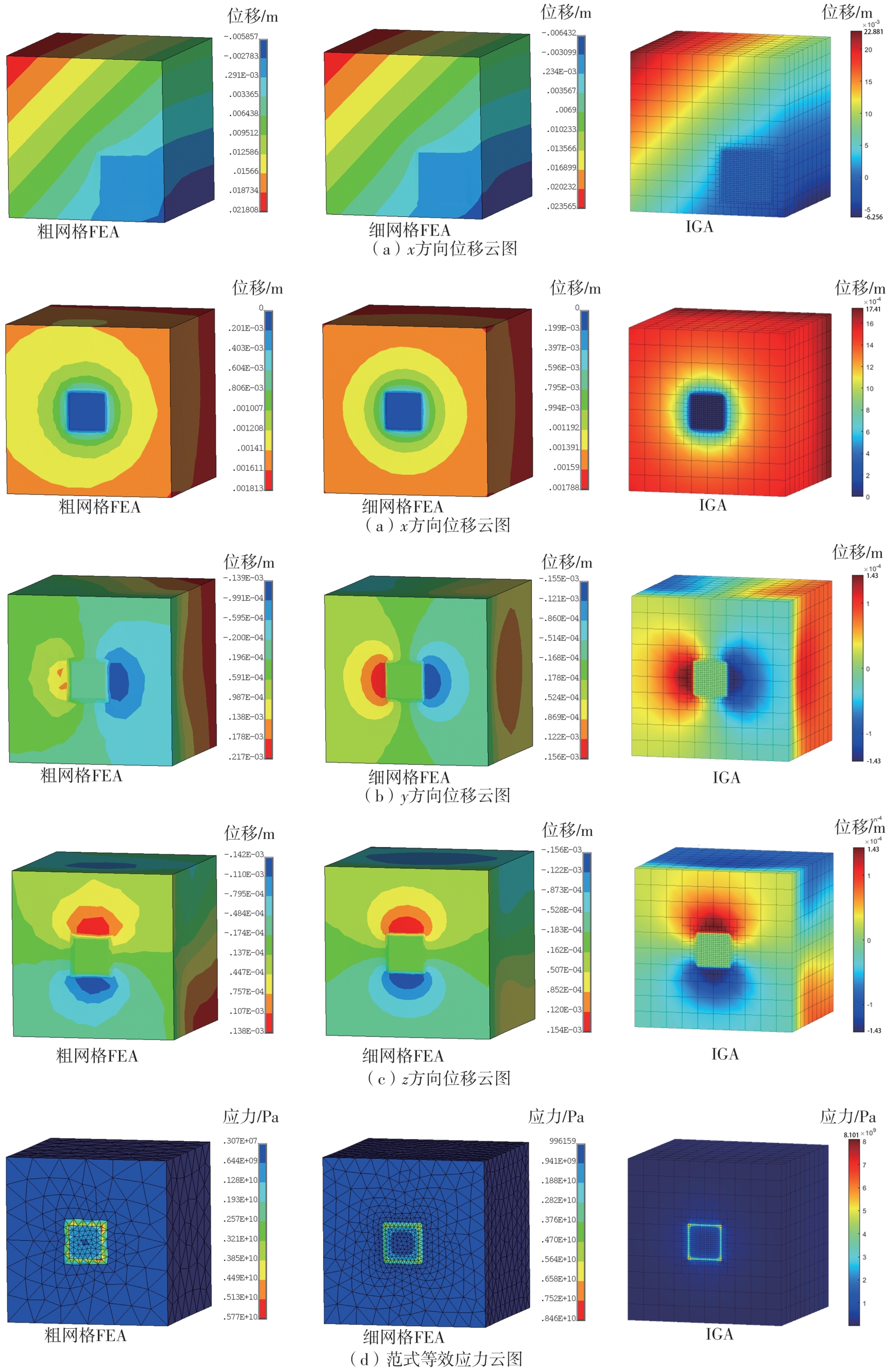
Results comparison and relative errors between FEA and IGA of examples 1 and 2"
| 算例 | 参数名称 | 符号及单位 | 粗网格FEA结果 | 细网格FEA结果 | IGA结果 | 相对误差1/% | 相对误差2/% |
|---|---|---|---|---|---|---|---|
| 算例1 | 位移 | sx /m | 2.01 × 10-3 | 2.08 × 10-3 | 2.07 × 10-3 | -3.37 | -0.48 |
| sy /m | -1.49 × 10-4 | -1.88 × 10-4 | -1.68 × 10-4 | -20.74 | -10.64 | ||
| sz /m | -1.54 × 10-4 | -1.87 × 10-4 | -1.68 × 10-4 | -17.65 | -10.16 | ||
| 应力 | σ/Pa | 6.27 × 109 | 9.52 × 109 | 9.45 × 109 | -34.14 | -0.74 | |
| 算例2 | 位移 | sx /m | 3.52 × 10-2 | 3.64 × 10-2 | 3.66 × 10-2 | -3.30 | 0.55 |
| sy /m | -2.21 × 10-2 | -2.30 × 10-2 | -2.31 × 10-2 | -3.91 | 0.43 | ||
| sz /m | -2.21 × 10-2 | -2.29 × 10-2 | -2.31 × 10-2 | -3.49 | 0.87 | ||
| 应力 | σ/Pa | 2.93 × 1010 | 4.51 × 1010 | 4.47 × 1010 | -35.03 | -0.89 |
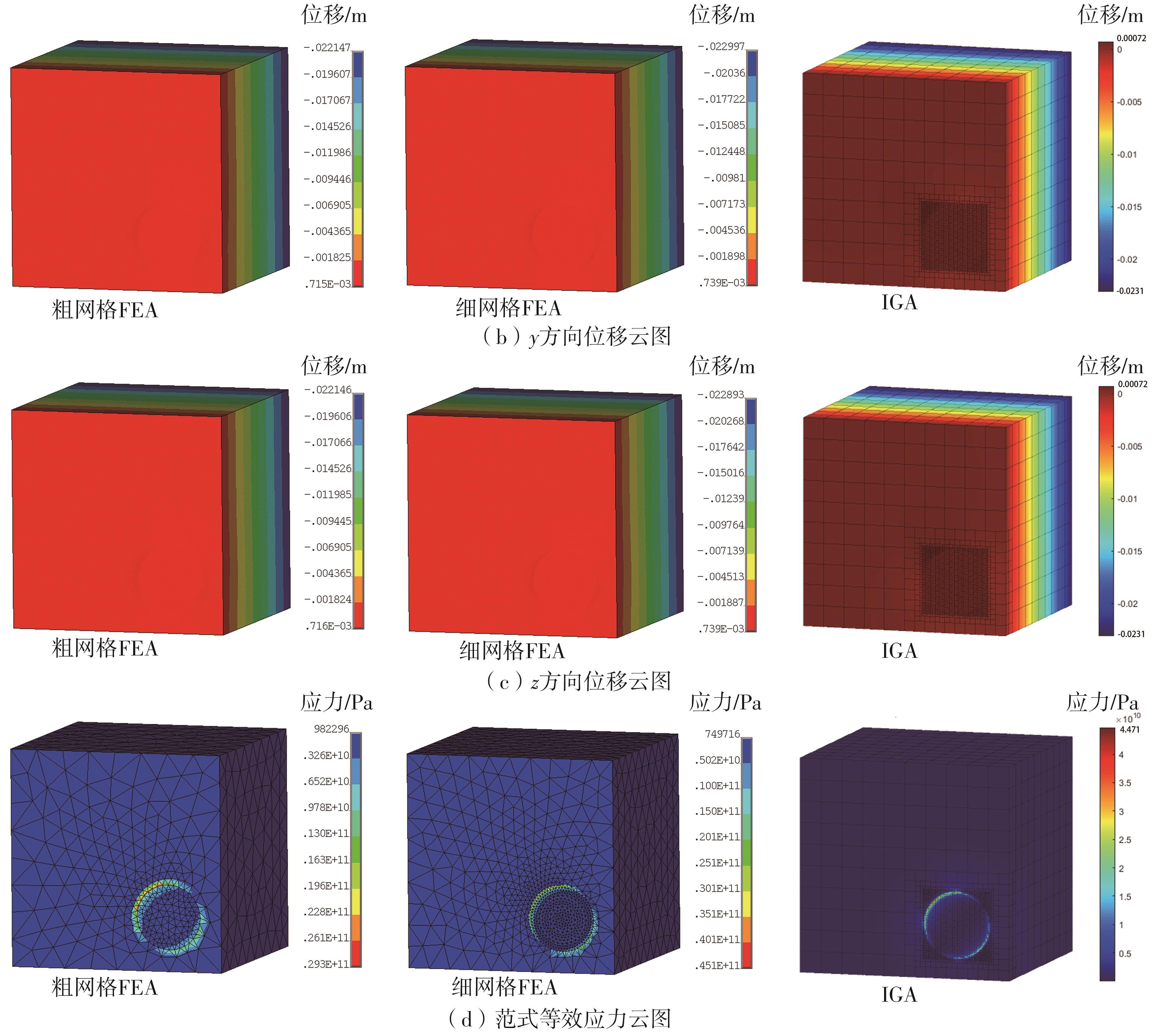
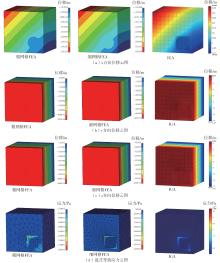
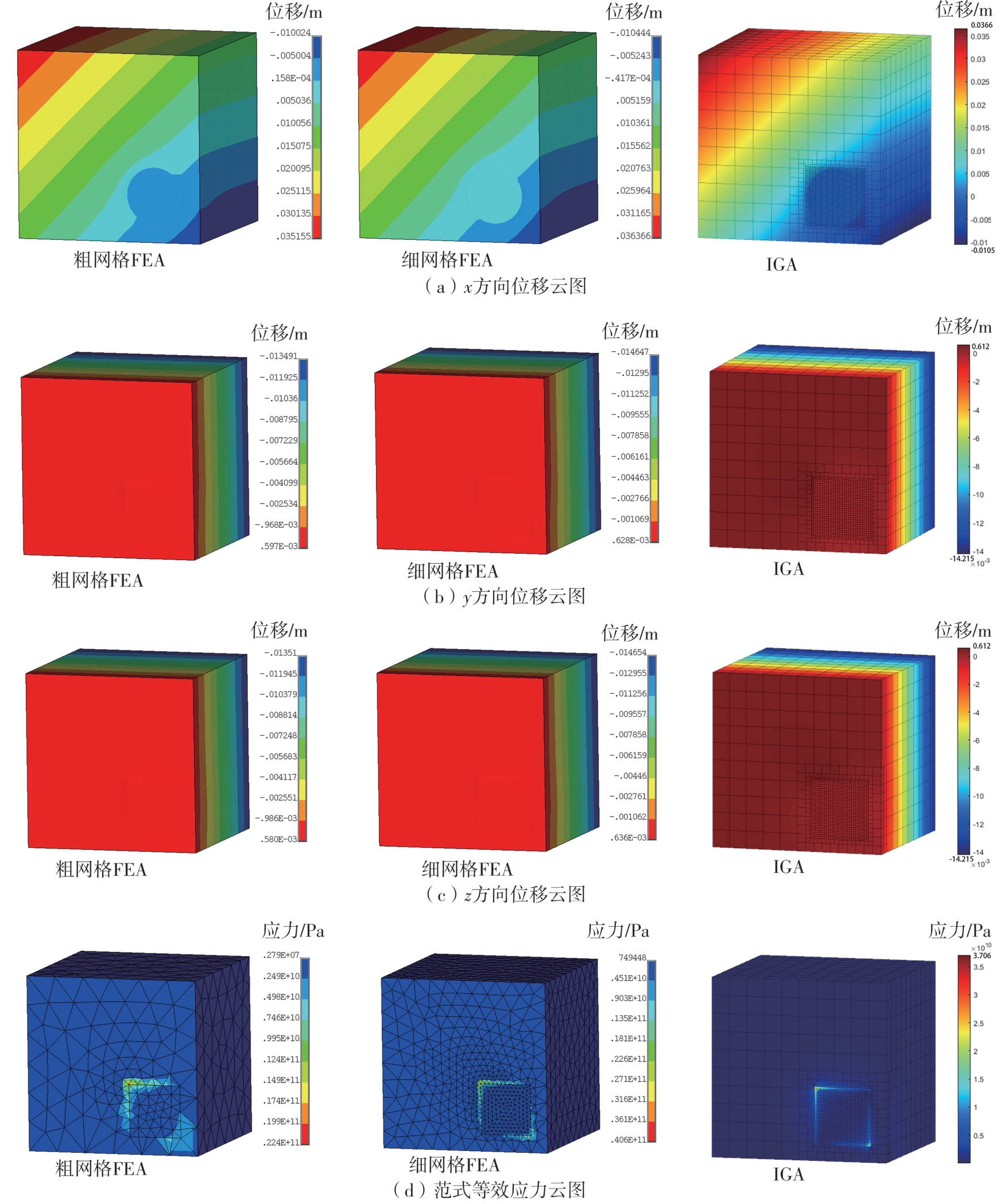
Table 4
Results comparison and relative errors between FEA and IGA of examples 3 and 4"
| 算例 | 参数名称 | 符号及单位 | 粗网格FEA结果 | 细网格FEA结果 | IGA结果 | 相对误差1/% | 相对误差2/% |
|---|---|---|---|---|---|---|---|
| 算例3 | 位移 | sx /m | 1.81 × 10-3 | 1.79 × 10-3 | 1.74 × 10-3 | 1.12 | -2.79 |
| sy /m | 2.17 × 10-4 | 1.56 × 10-4 | 1.43 × 10-4 | 39.10 | -8.33 | ||
| sz /m | -1.42 × 10-4 | -1.56 × 10-4 | -1.43 × 10-4 | -8.97 | -8.33 | ||
| 应力 | σ/Pa | 5.77 × 109 | 8.46 × 109 | 8.10 × 109 | -31.80 | -4.26 | |
| 算例4 | 位移 | sx /m | 2.18 × 10-2 | 2.36 × 10-2 | 2.29 × 10-2 | -7.63 | -2.97 |
| sy /m | -1.35 × 10-2 | -1.46 × 10-2 | -1.42 × 10-2 | -7.53 | -2.74 | ||
| sz /m | -1.35 × 10-2 | -1.47 × 10-2 | -1.42 × 10-2 | -8.16 | -3.40 | ||
| 应力 | σ/Pa | 2.24 × 1010 | 4.06 × 1010 | 3.71 × 1010 | -44.83 | -8.62 |
| 1 | 乔发杰 .基于等几何分析的大变形梁结构仿真分析算法[D].大连:大连理工大学,2022. |
| 2 | 郭玉杰,吴晗浪,李薇,等 .基于等几何分析的参数化曲梁结构非线性动力学降阶模型研究[J].工程力学,2022,39(8):31-48. |
| GUO Yujie, WU Hanlang, LI Wei,et al .Model order reduction for nonlinear dynamic analysis of parameterized curved beam structures based on isogeometric analysis[J].Engineering Mechanics,2022,39(8):31-48. | |
| 3 | 金灵智,王禹,郝鹏,等 .加筋路径驱动的板壳自适应等几何屈曲分析[J].力学学报,2023,55(5):1151-1164. |
| JIN Lingzhi, WANG Yu, HAO Peng,et al .Adaptive isogeometric buckling analysis of stiffened panels driven by stiffener paths[J].Chinese Journal of Theoretical and Applied Mechanics,2023,55(5):1151-1164. | |
| 4 | 费建国,罗会信,左兵权,等 .雷诺方程的数值计算方法概述[J].润滑与密封,2020,45(4):130-140. |
| FEI Jianguo, LUO Huixin, ZUO Bingquan,et al .An overview of numerical methods for Reynolds equation[J].Lubrication Engineering,2020,45(4):130-140. | |
| 5 | 于嘉瑞,岳宝增,李晓玉 .燃料大幅晃动等几何分析仿真及航天器耦合动力学研究[J].力学学报,2023,55(2):476-486. |
| YU Jiarui, YUE Baozeng, LI Xiaoyu .Study on isogeometric analysis for large-amplitude propellant sloshing and spacecraft coupled dynamics[J].Chinese Journal of Theoretical and Applied Mechanics,2023,55(2):476-486. | |
| 6 | PEROTTO S, BELLINI G, BALLARIN F,et al .Isogeometric hierarchical model reduction for advection-diffusion process simulation in microchannels[M]∥CHINESTA F,CUETO E,PAYAN Y,et al eds.Reduced Order Models for the Biomechanics of Living Organs.Pittsburgh:Academic Press,2023:197-211. |
| 7 | 张洪海,莫蓉,万能 .应用等几何配点法求解电磁涡流场问题[J].计算机辅助设计与图形学学报,2019,31(3):496-503. |
| ZHANG Honghai, MO Rong, WAN Neng .Solving eddy current fields with isoeometric collocation method[J].Journal of Computer-Aided Design & Computer Graphics,2019,31(3):496-503. | |
| 8 | ASHOUR M, VALIZADEH N, RABCZUK T .Isogeometric analysis for a phase-field constrained optimization problem of morphological evolution of vesicles in electrical fields[J].Computer Methods in Applied Mechanics and Engineering,2021,377:113669/1-27. |
| 9 | 刘涛,张顺琦,刘庆运 .热环境下压电功能梯度板的非线性等几何建模与主动控制研究[J].振动与冲击,2023,42(8):38-50. |
| LIU Tao, ZHANG Shunqi, LIU Qingyun .Nonlinear isogeometric modeling and active control of piezoelectric functionally graded plates in thermal environment[J].Journal of Vibration and Shock,2023,42(8):38-50. | |
| 10 | 高建伟,陈龙 .基于等几何分析的股骨模型静力学分析[J].计算机仿真,2015,32(5):340-343. |
| GAO Jianwei, CHEN Long .Construction and static analysis of femur based on IGA[J].Computer Simulation,2015,32(5):340-343. | |
| 11 | 产启平,陈龙 .基于等几何分析的非均质股骨近端模型的受力分析[J].电子科技,2018,31(2):15-19. |
| CHAN Qiping, CHEN Long .Stress analysis of heterogeneous femoral proximal model by using isogeometric analysis[J].Electronic Science and Technology,2018,31(2):15-19. | |
| 12 | 马书豪 .心脏瓣膜流固耦合问题的等几何分析快速仿真方法[D].杭州:杭州电子科技大学,2022. |
| 13 | COSTANTINI P, MANNI C, PELOSI F,et al .Quasi-interpolation in isogeometric analysis based on generalized B-splines[J].Computer Aided Geometric Design,2010,27(8):656-668. |
| 14 | 陈涛,莫蓉,万能 .等几何分析中Dirichlet边界条件的配点施加方法[J].机械工程学报,2012,48(5):157-164. |
| CHEN Tao, MO Rong, WAN Neng .Imposing Dirichlet boundary conditions with point collocation method in isogeometric analysis[J].Journal of Mechanical Engineering,2012,48(5):157-164. | |
| 15 | 陈涛,莫蓉,万能,等 .等几何分析中采用Nitsche法施加位移边界条件[J].力学学报,2012,44(2):371-381. |
| CHEN Tao, MO Rong, WAN Neng,et al .Imposing displacement boundary conditions with Nitsche’s method in isogeometric analysis[J].Chinese Journal of Theoretical and Applied Mechanics,2012,44(2):371-381. | |
| 16 | HÖLLIG K, REIF U, WIPPER J .Weighted extended B-spline approximation of Dirichlet problems[J].SIAM Journal on Numerical Analysis,2001,39(2):442-462. |
| 17 | SHAPIRO V .Theory of R-functions and applications[R].Ithaca:Cornell University,1988. |
| 18 | SHAPIRO V, TSUKANOV I .Meshfree simulation of deforming domains[J].Computer-Aided Design,1999,31(7):459-471. |
| 19 | TSUKANOV I, SHAPIRO V, ZHANG S .A meshfree method for incompressible fluid dynamics problems[J].International Journal for Numerical Methods in Engineering,2003,58(1):127-158. |
| 20 | SHAPIRO V, TSUKANOV I .The architecture of SAGE - a meshfree system based on RFM[J].Engineering with Computers,2002,18:295-311. |
| 21 | ZHANG W, ZHAO L, CAI S .Shape optimization of Dirichlet boundaries based on weighted B-spline finite cell method and level-set function[J].Computer Methods in Applied Mechanics and Engineering,2015,294:359-383. |
| 22 | VERSCHAEVE J C G .A weighted extended B-spline solver for bending and buckling of stiffened plates[J].Thin-Walled Structures,2016,107:580-596. |
| 23 | BURLA R K, KUMAR A V .Implicit boundary method for analysis using uniform B‐spline basis and structured grid[J].International Journal for Numerical Methods in Engineering,2008,76(13):1993-2028. |
| 24 | KUMAR A V, PADMANABHAN S, BURLA R .Implicit boundary method for finite element analysis using non‐conforming mesh or grid[J].International Journal for Numerical Methods in Engineering,2008,74(9):1421-1447. |
| 25 | COTTRELL J A, HUGHES T J R, REALI A .Studies of refinement and continuity in isogeometric structural analysis[J].Computer Methods in Applied Mechanics and Engineering,2007,196(41-44):4160-4183. |
| 26 | SEDERBERG T W, ZHENG J, BAKENOV A,et al .T-splines and T-NURCCs[J].ACM Transactions on Graphics(TOG),2003,22(3):477-484. |
| 27 | SEDERBERG T W, CARDON D L, FINNIGAN G T,et al .T-spline simplification and local refinement[J].ACM Transactions on Graphics(TOG),2004,23(3):276-283. |
| 28 | BUFFA A, CHO D, SANGALLI G .Linear independence of the T-spline blending functions associated with some particular T-meshes[J].Computer Methods in Applied Mechanics and Engineering,2010,199(23/24):1437-1445. |
| 29 | FORSEY D R, BARTELS R H .Hierarchical B-spline refinement[C]∥Proceedings of the 15th Annual Conference on Computer Graphics and Interactive Techniques.New York:Association for Computing Machinery,1988:205-212. |
| 30 | FORSEY D R, BARTELS R H .Surface fitting with hie-rarchical splines[J].ACM Transactions on Graphics (TOG),1995,14(2):134-161. |
| 31 | LI X, CHEN F, KANG H,et al .A survey on the local refinable splines[J].Science China Mathematics,2016,59(4):617-644. |
| 32 | GARAU E M, VÁZQUEZ R .Algorithms for the implementation of adaptive isogeometric methods using hierarchical B-splines[J].Applied Numerical Mathe-matics,2018,123:58-87. |
| 33 | KURU G, VERHOOSEL C V, VAN DER ZEE K G,et al .Goal-adaptive isogeometric analysis with hierarchical splines[J].Computer Methods in Applied Mechanics and Engineering,2014,270:270-292. |
| 34 | SCHMIDT M, NOËL L, DOBLE K,et al .Extended isogeometric analysis of multi-material and multi-physics problems using hierarchical B-splines[J].Computational Mechanics,2023,71(6):1179-1203. |
| 35 | KHOEI A R .Extended finite element method:theory and applications[M].Hoboken:John Wiley & Sons,2014. |
| [1] | Wang Hong Yuan Hong. Application of Green Quasifunction Method in Elastic Torsion [J]. Journal of South China University of Technology(Natural Science Edition), 2004, 32(11): 86-88. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||