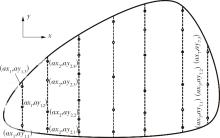
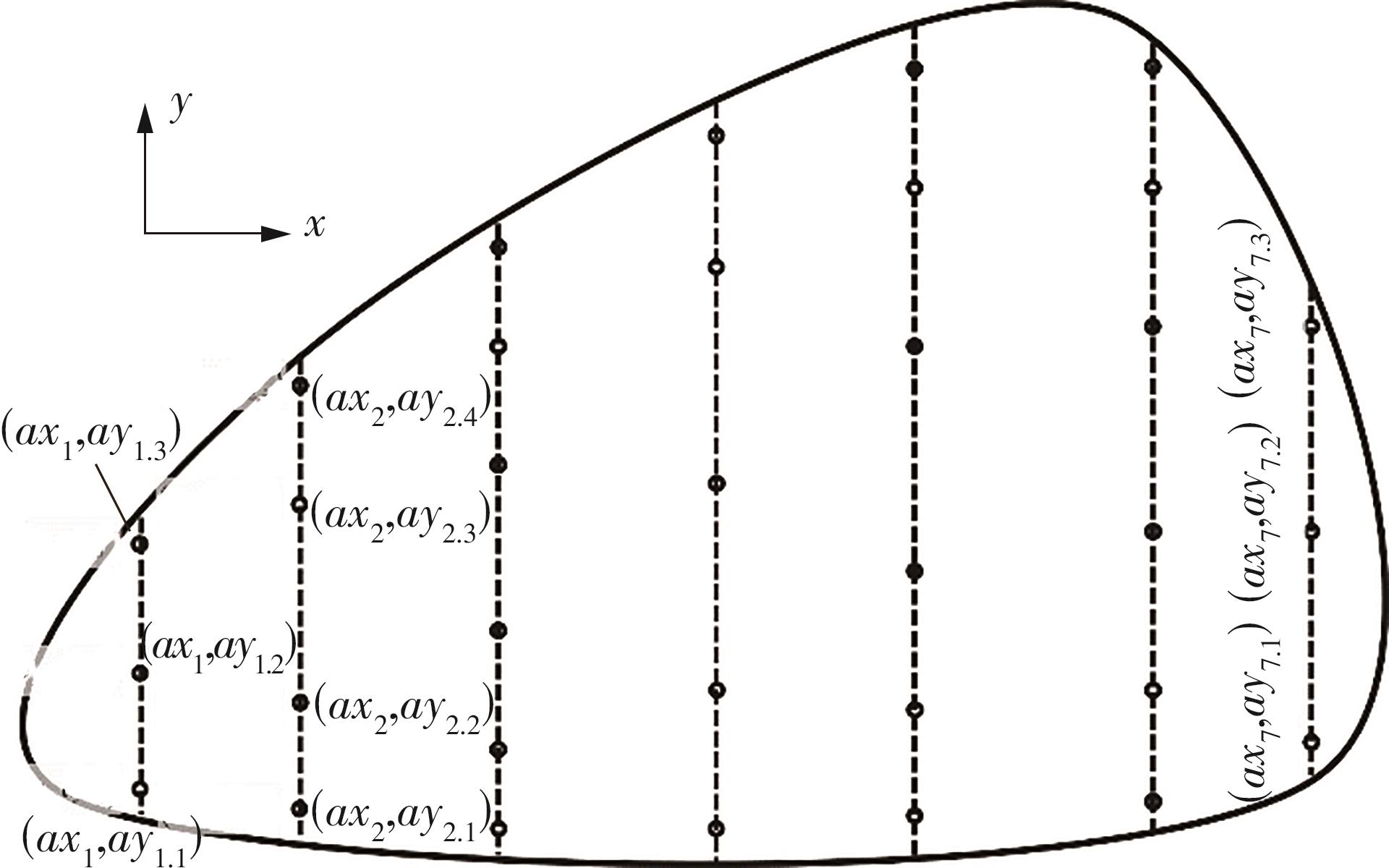
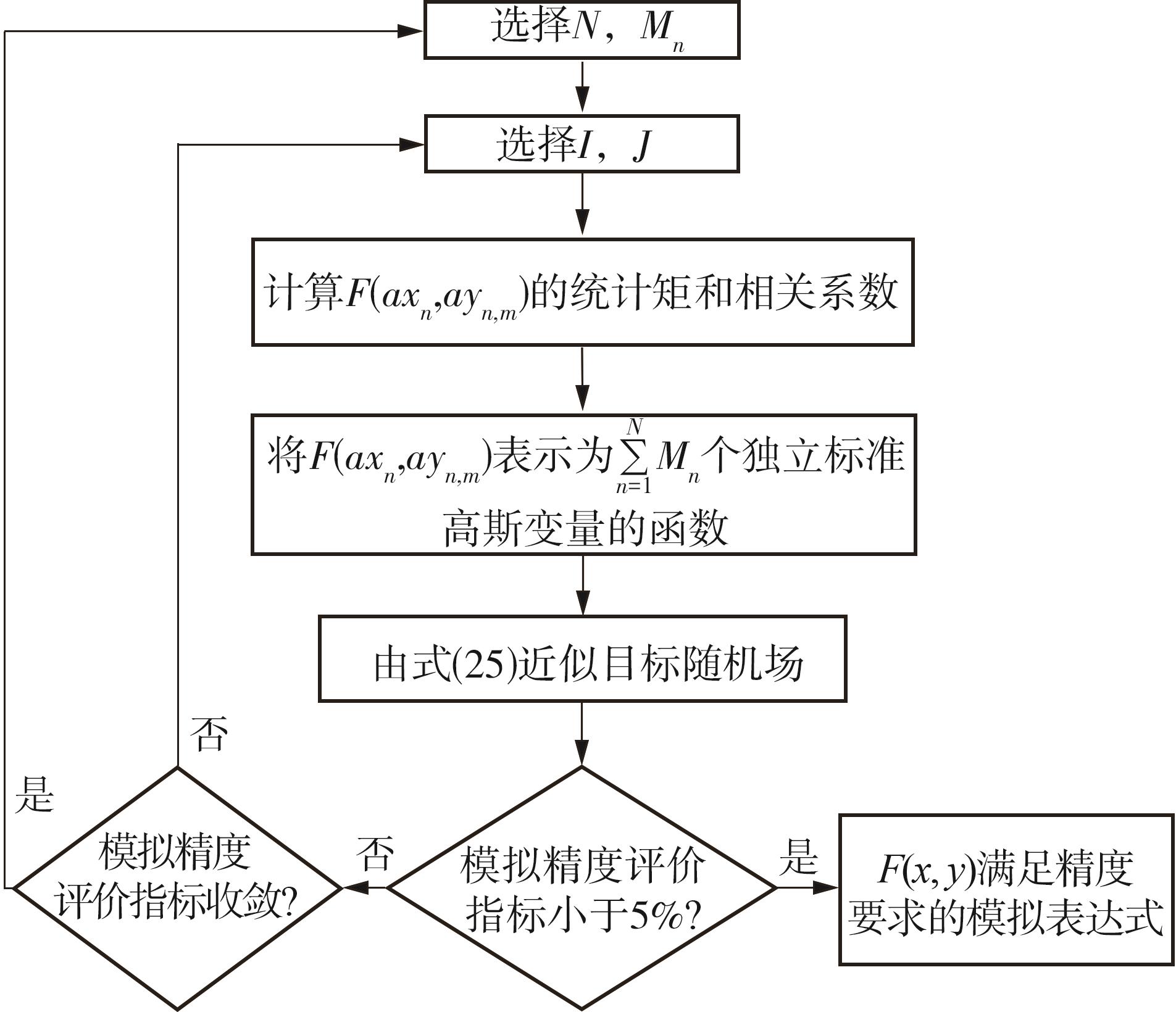
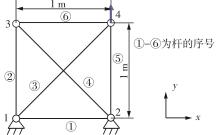
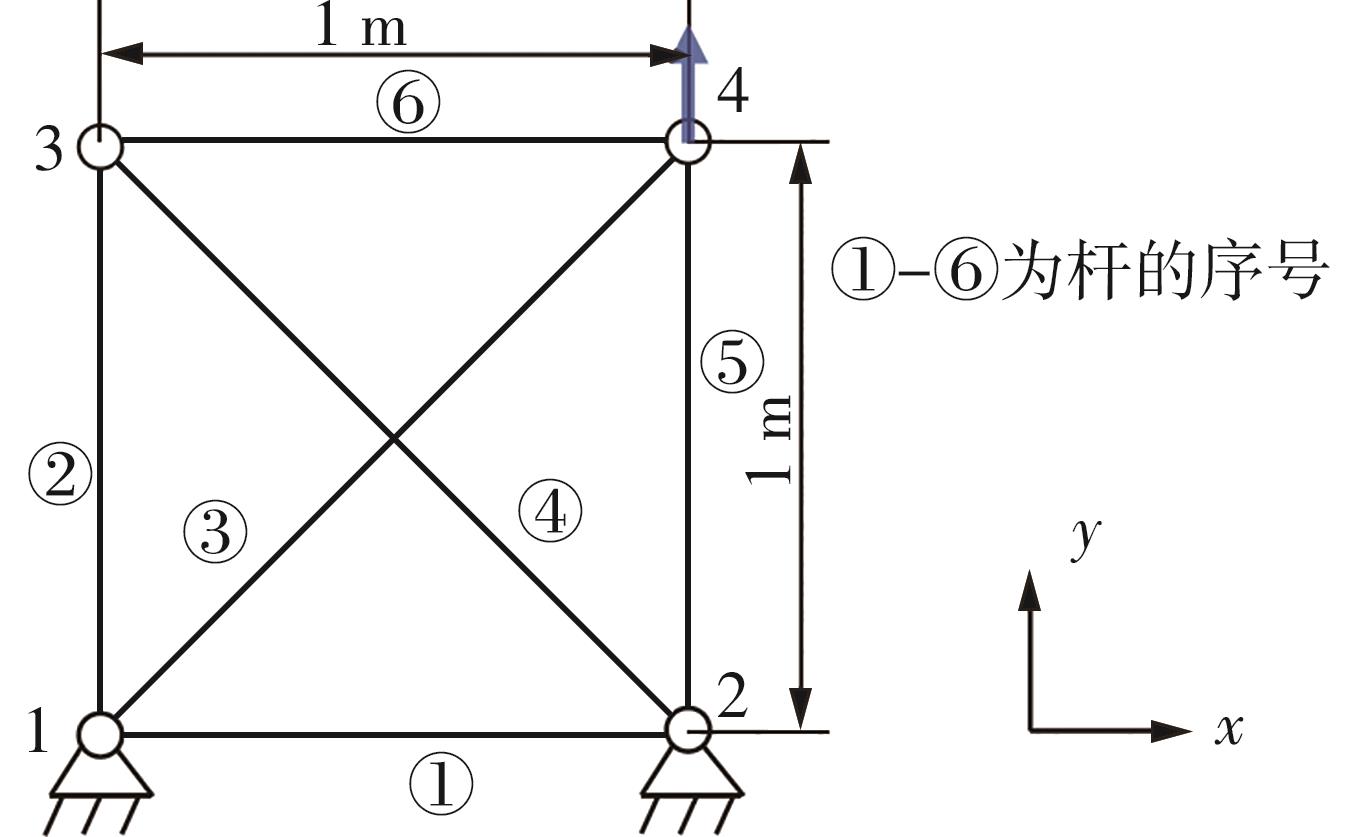
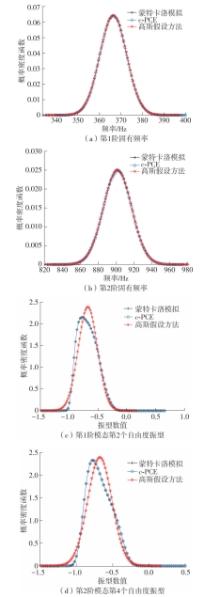
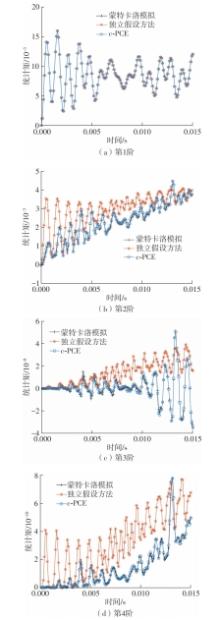
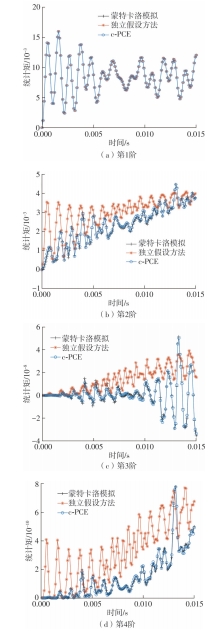
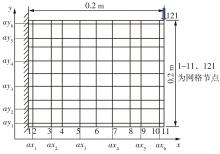
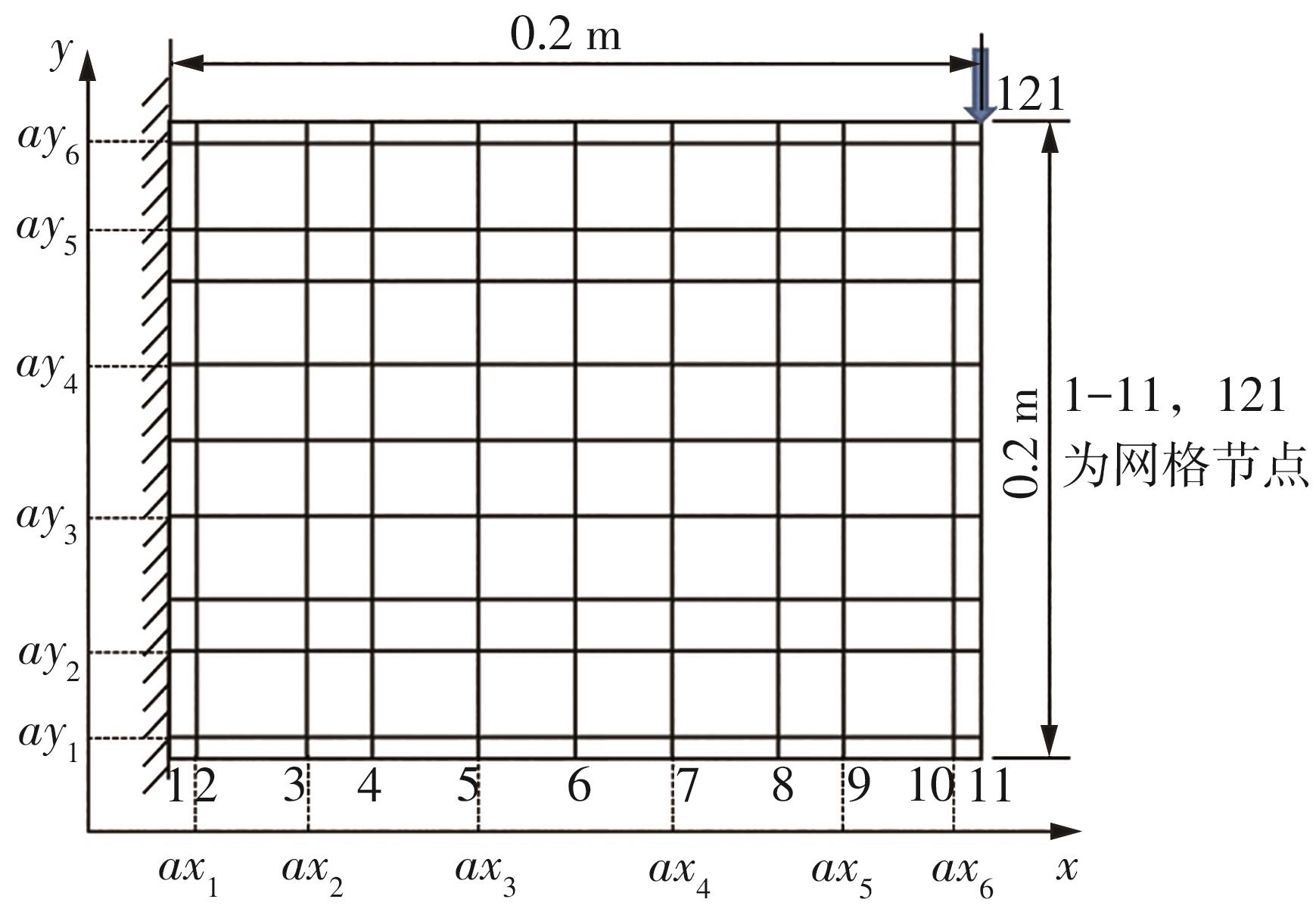
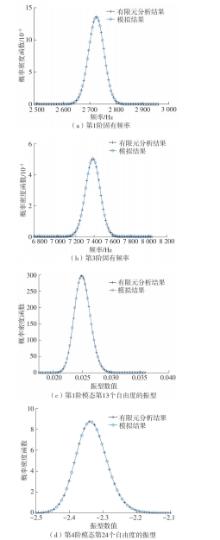
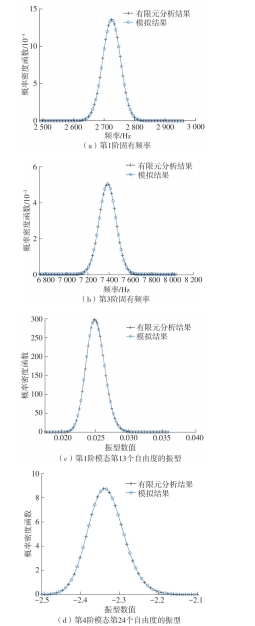
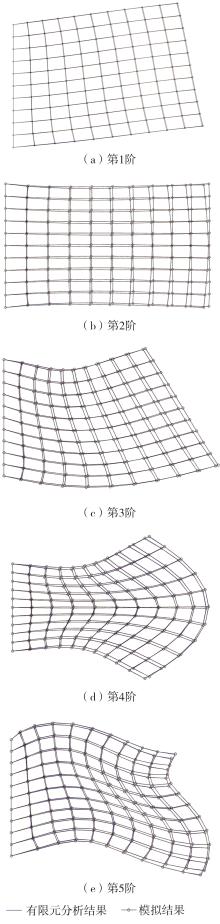
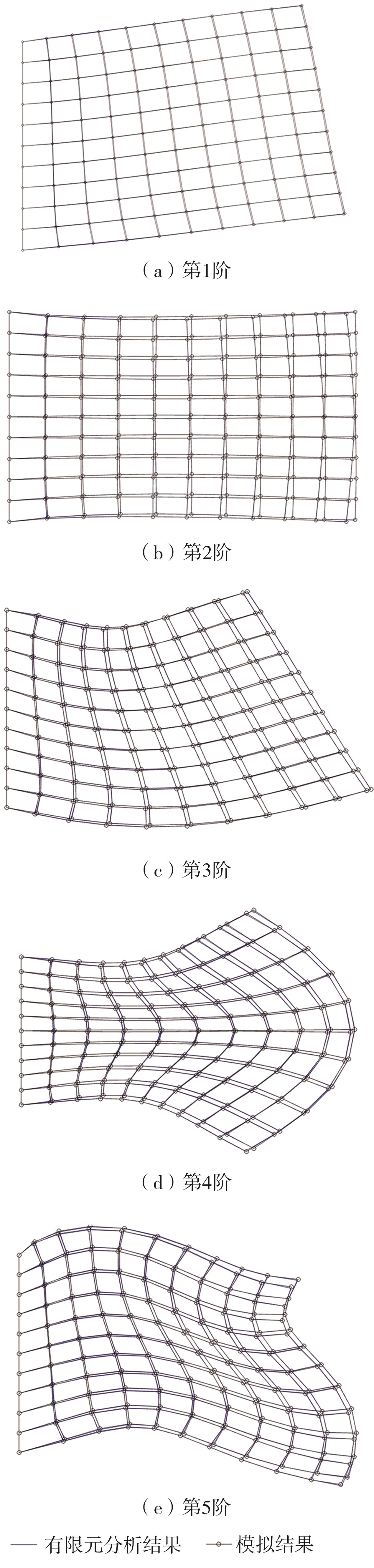
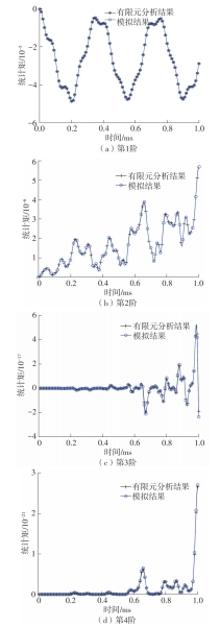
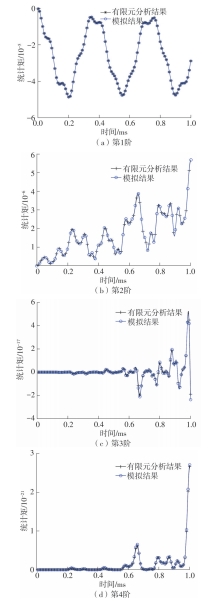
Journal of South China University of Technology(Natural Science Edition) ›› 2024, Vol. 52 ›› Issue (9): 81-92.doi: 10.12141/j.issn.1000-565X.230582
• Mechanical Engineering • Previous Articles Next Articles
Non-Gaussian Modal Parameters Simulation Methods for Uncertainty Structures
PING Menghao( ), ZHANG Wenhua, TANG Liang(
), ZHANG Wenhua, TANG Liang( )
)
- Institute of Technology,Beijing Forestry University,Beijing 100083,China
-
Received:2023-09-14Online:2024-09-25Published:2024-01-26 -
Contact:唐亮(1982—),女,博士,教授,主要从事人体损伤生物力学、智能驾驶汽车安全性、汽车结构耐撞性与轻量化等研究。 E-mail:happyliang@bjfu.edu.cn -
About author:平梦浩(1992—),男,博士,讲师,主要从事结构不确定性度量、贝叶斯估计方法等研究。E-mail: pingmenghao@bjfu.edu.cn -
Supported by:the National Natural Science Foundation of China(51975057)
CLC Number:
Cite this article
PING Menghao, ZHANG Wenhua, TANG Liang. Non-Gaussian Modal Parameters Simulation Methods for Uncertainty Structures[J]. Journal of South China University of Technology(Natural Science Edition), 2024, 52(9): 81-92.
share this article
| 1 | BATHE K J .Finite element procedures[M].Englewood Cliffs:Klaus-Jurgen Bathe,2006. |
| 2 | ALVIN K F, ROBERTSON A N, REICH G W,et al .Structural system identification:from reality to models[J].Computers & Structures,2003,81(12):1149-1176. |
| 3 | YANG T, FAN S H, LIN C S .Joint stiffness identification using FRF measurements[J].Computers & Structures,2003,81(28/29):2549-2556. |
| 4 | GOLLER B, BROGGI M, CALVI A,et al .A stochastic model updating technique for complex aerospace structures[J].Finite Elements in Analysis and Design,2011,47(7):739-752. |
| 5 | YUEN K V, AU S K, BECK J L .Two-stage structural health monitoring approach for phase i benchmark studies[J].Journal of Engineering Mechanics-ASCE,2004,130(1):16-33. |
| 6 | LAM H F, YIN T .Statistical detection of multiple cracks on thin plates utilizing dynamic response[J].Engineering Structures,2010,32(10):3145-3152. |
| 7 | ZHU H P, LI L, HE X Q .Damage detection method for shear buildings using the changes in the first mode shape slopes[J].Computers & Structures,2011,89(9/10):733-743. |
| 8 | SINGH B N, YADAV D, IYENGAR N G R .Natural frequencies of composite plates with random material properties using higher-order shear deformation theory[J].International Journal of Mechanical Sciences,2001,43(10):2193-2214. |
| 9 | LIN S C .The probabilistic approach for rotating Timoshenko beams[J].International Journal of Solids and Structures,2001,38(40/41):7197-7213. |
| 10 | VAN DEN NIEUWENHOF B, COYETT J P .Modal approaches for the stochastic finite element analysis of structures with material and geometric uncertainties[J].Computer Methods in Applied Mechanics and Engineering,2003,192(33/34):3705-3729. |
| 11 | GAO W, ZHANG N, JI J .A new method for random vibration analysis of stochastic truss structures[J].Finite Elements in Analysis and Design,2009,45(3):190-199. |
| 12 | GAO W, ZHANG N, DAI J .A stochastic quarter-car model for dynamic analysis of vehicles with uncertain parameters[J].Vehicle System Dynamics,2008,46(12):1159-1169. |
| 13 | PEETERS B, DE R G .Stochastic system identification for operational modal analysis:a review[J].Journal of Dynamic Systems,Measurement and Control,2001,123(4):659-667. |
| 14 | BRINCKER R, ZHANG L, ANDERSEN P .Modal identification of output-only systems using frequency domain decomposition[J].Smart Materials and Structures,2001,10(3):441-445. |
| 15 | MAGALHAES F, CUNHA A .Explaining operational modal analysis with data from an arch bridge[J].Mechanical Systems and Signal Processing,2011,25(5):1431-1450. |
| 16 | AU S K .Fast bayesian ambient modal identification in the frequency domain,Part I:posterior most probable value[J].Mechanical Systems and Signal Processing,2012,26(1):60-75. |
| 17 | AU S K .Fast bayesian ambient modal identification in the frequency domain,Part II:posterior uncertainty[J].Mechanical Systems and Signal Processing,2012,26(1):76-90. |
| 18 | AU S K, ZHANG F L, NI Y C .Bayesian operational modal analysis:theory,computation,practice[J].Computers & Structures,2013,126(28):3-14. |
| 19 | BEHMANESH I, MOAVENI B, LOMBAERT G,et al .Hierarchical bayesian model updating for structural identification[J].Mechanical Systems and Signal Processing,2015(64/65):360-376. |
| 20 | VANIK M W, BECK J L, AU S K .Bayesian probabilistic approach to structural health monitoring[J].Journal of Engineering Mechanics,2000,126(7):738-745. |
| 21 | YUEN K V, BECK J L, KATAFYGIOTIS L S .Efficient model updating and health monitoring methodology using incomplete modal data without mode matching[J].Structural Control & Health Monitoring,2010,13(1):91-107. |
| 22 | SOHN H, LAW K H .A bayesian probabilistic approach for structure damage detection[J].Earthquake Engineering & Structural Dynamics,2015,26(12):1259-1281. |
| 23 | SAKAMOTO S, GHANEM R .Polynomial chaos decomposition for the simulation of non-Gaussian nonstationary stochastic processes[J].Journal of Engineering Mechanics,2002,128(2):190-201. |
| 24 | PING M.H, HAN X, JIANG C,et al .A time-variant uncertainty propagation analysis method based on a new technique for simulating non-Gaussian stochastic processes[J].Mechanical Systems and Signal Processing,2021,150:107299. |
| 25 | XIONG F, Greene S, CHEN W,et al .A new sparse grid based method for uncertainty propagation[J].Structural and Multidisciplinary Optimization,2010,41(3):335-349. |
| 26 | JIA X Y, JIANG C, FU C M,et al .Uncertainty propagation analysis by an extended sparse grid technique[J].Frontiers of Mechanical Engineering,2019,14(1):33-46. |
| 27 | WU J, ZHANG D, JIANG C,et al .On reliability analysis method through rotational sparse grid nodes[J].Mechanical Systems and Signal Processing,147:107106. |
| 28 | GAO W, CHEN J, CUI M,et al .Dynamic response analysis of linear stochastic truss structures under stationary random excitation[J].Journal of Sound and Vibration,2005,281(1/2):311-321. |
| 29 | XIU D, KARNIADAKIS G E .The wiener--askey polynomial chaos for stochastic differential equations[J].SIAM Journal on Scientific Computing,2002,24(2):619-644. |
| 30 | ZHANG J, ELLINGWOOD B .Orthogonal series expansions of random fields in reliability analysis[J].Journal of Engineering Mechanics,1994,120(12):2660-2677. |
| 31 | YANG C, DURAISWAMI R, GUMEROV N A,et al .Improved fast gauss transform and efficient kernel density estimation[C]∥Proceedings of the Ninth IEEE International Conference on Computer Vision.[S.l.]:IEEE,2008. |
| 32 | KRISTAN M, LEONARDIS A, SKOCAJ D .Multivariate online kernel density estimation with Gaussian kernels[J].Pattern Recognition,2011,44(10/11):2630-2642. |
| [1] | ZHENG Sifan, WANG Weixing, HE Zhanhua, et al. Research on Swing Amplitude Detection of Automobile Wiper with Two Granularity Optical Flow Manifold Learning#br# [J]. Journal of South China University of Technology (Natural Science Edition), 2020, 48(1): 123-132. |
| [2] | Wang Qiang Su Cheng. Stationarity and Ergodicity of Random Motorcade on Highway Bridge [J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(10): 8-15. |
| [3] | Sun Ji-feng Ouyang Jin-hua. Video Segmentation Algorithm Based on Partitioning-Processing Conditional Random Field [J]. Journal of South China University of Technology(Natural Science Edition), 2012, 40(6): 43-47. |
| [4] | Min Hua-qing Lü Ju-mei Luo Rong-hua Chen Cong. Adaptive Shadow Detection Based on GMM and MRF [J]. Journal of South China University of Technology (Natural Science Edition), 2011, 39(7): 115-120. |
| [5] | Luo Rong-hua Min Hua-qing. Hybrid Conditional Random Field for Multi-Object Tracking of Mobile Robot [J]. Journal of South China University of Technology (Natural Science Edition), 2011, 39(5): 61-67. |
| [6] | Su Cheng Xu Rui Fan Xue-ming. Local Average Method Based on Curved-Side Elements for Discretization of 2D Random Fields [J]. Journal of South China University of Technology (Natural Science Edition), 2008, 36(3): 104-107,120. |
| [7] | Yu Jiang-de Fan xiao-zhong yin ji-hao. Information Extraction from Chinese Research Papers Based on Conditional Random Fields [J]. Journal of South China University of Technology (Natural Science Edition), 2007, 35(9): 90-94,106. |
| [8] | Xu Zhi-liang Xie Sheng-li. An Adaptive Deblocking Algorithm Based on M RF [J]. Journal of South China University of Technology (Natural Science Edition), 2005, 33(7): 15-19. |
| [9] | Su Cheng Fan Xue-ming Yan Quan-sheng . Stochastic Analysis of Axially-loaded Bars by Singular Points Outside Domain Method [J]. Journal of South China University of Technology(Natural Science Edition), 2003, 31(9): 86-89. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||