不确定性结构的非高斯模态参数模拟方法

doi:10.12141/j.issn.1000-565X.230582

华南理工大学学报(自然科学版) ›› 2024, Vol. 52 ›› Issue (9): 81-92.doi: 10.12141/j.issn.1000-565X.230582

不确定性结构的非高斯模态参数模拟方法

平梦浩(), 张文华, 唐亮()

北京林业大学工学院，北京 100083

收稿日期:2023-09-14 出版日期:2024-09-25 发布日期:2024-01-26
通信作者: 唐亮（1982—），女，博士，教授，主要从事人体损伤生物力学、智能驾驶汽车安全性、汽车结构耐撞性与轻量化等研究。 E-mail:happyliang@bjfu.edu.cn
作者简介:平梦浩（1992—），男，博士，讲师，主要从事结构不确定性度量、贝叶斯估计方法等研究。E-mail： pingmenghao@bjfu.edu.cn
基金资助:
国家自然科学基金资助项目(51975057);北京林业大学中央高校基本科研业务费专项资金资助项目(BLX202228)

Non-Gaussian Modal Parameters Simulation Methods for Uncertainty Structures

PING Menghao(), ZHANG Wenhua, TANG Liang()

Institute of Technology，Beijing Forestry University，Beijing 100083，China

Received:2023-09-14 Online:2024-09-25 Published:2024-01-26
Contact: 唐亮（1982—），女，博士，教授，主要从事人体损伤生物力学、智能驾驶汽车安全性、汽车结构耐撞性与轻量化等研究。 E-mail:happyliang@bjfu.edu.cn
About author:平梦浩（1992—），男，博士，讲师，主要从事结构不确定性度量、贝叶斯估计方法等研究。E-mail： pingmenghao@bjfu.edu.cn
Supported by:
the National Natural Science Foundation of China(51975057)

摘要/Abstract

摘要：

结构不确定性广泛存在于实际工程问题中，考虑不确定因素对模态参数的影响对提升结构动力学分析的鲁棒性具有重要意义。在涉及不确定性线性结构随机模态参数求解或估计的方法中，模态参数通常被视为服从高斯分布，它们之间的相关性也通常被忽略。然而，随机模态参数的高斯和独立性假设会造成模拟误差，影响结构动力学响应预测的鲁棒性。针对这一问题，分别针对离散结构和连续结构提出了两种随机模态参数模拟方法。对于离散结构，由于振型是离散的，随机模态参数被视为相关随机变量，根据它们的统计特征，采用相关多项式混沌展开方法（c-PCE），将其表示为独立标准高斯变量的函数，可以实现非高斯性和相关性的模拟；对于连续结构，随机振型被视为相关随机场，利用改进的正交级数展开法可以将其表示为离散随机振型的函数，将它们与随机固有频率相结合，构造一组新的相关随机变量，采用c-PCE，可以实现利用标准高斯变量模拟振型随机场和随机频率。最后，分别以桁架结构和平板结构为例，考虑由材料参数波动引起的模态参数的非高斯性，利用提出的随机模态参数模拟方法，可以准确模拟模态参数的统计特征，进一步还能够预测结构的随机响应。证明了提出的方法对随机模态参数的模拟精度，以及考虑参数相关性的必要性。

Abstract:

Structural uncertainty is commonly encountered in practical structural engineering problems. Considering the impact of uncertain factors on modal parameters is of significant importance in enhancing the robustness of structural dynamic analysis. In most developed methods involving the solution or estimation of random modal parameters for linear structures, the modal parameters are usually seen as Gaussian variables, and correlation among them is not getting much attention. However, the Gaussian and independence assumptions of the random mode parameters create simulation errors, affecting the robustness of the structural dynamics response predictions. To address this issue, this study proposed two approaches for simulating random modal parameters of respective discrete and continuous structures. For a discrete structure, its mode shapes are discrete. The random modal parameters are treated as correlated random variables. The correlated polynomial chaos expansion (c-PCE) method was applied to simulate non-Gaussianity and correlation based on the statistics of modal parameters. For continuous structures, random mode shapes are seen as correlated random fields. They can be represented in terms of correlated random variables by using the improved orthogonal series expansion method. Then they were combined with random natural frequencies to constitute a set of correlation variables, which are enabled to be simulated using standard Gaussian variables by utilizing the c-PCE. Finally, taking the truss structure and the plate structure respectively as examples, considering the non-Gaussianism of the modal parameters caused by the fluctuation of material parameters, the proposed random mode parameters can accurately simulate the statistical characteristics of the modal parameters, and further predict the random response of the structure. The simulation results verify the simulation accuracy of the proposed method for the random mode parameters and the necessity to consider the parameter correlations.

Key words: random modal parameter, correlated variable, random field, polynomial chaos expansion, orthogonal series expansion

中图分类号:

TB114

平梦浩, 张文华, 唐亮. 不确定性结构的非高斯模态参数模拟方法[J]. 华南理工大学学报(自然科学版), 2024, 52(9): 81-92.

PING Menghao, ZHANG Wenhua, TANG Liang. Non-Gaussian Modal Parameters Simulation Methods for Uncertainty Structures[J]. Journal of South China University of Technology(Natural Science Edition), 2024, 52(9): 81-92.

图/表 11

图1

图2

图3

图4

图5

图6

图7

图8

图9

图10

图11

参考文献 32

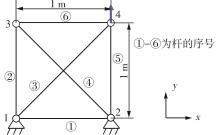
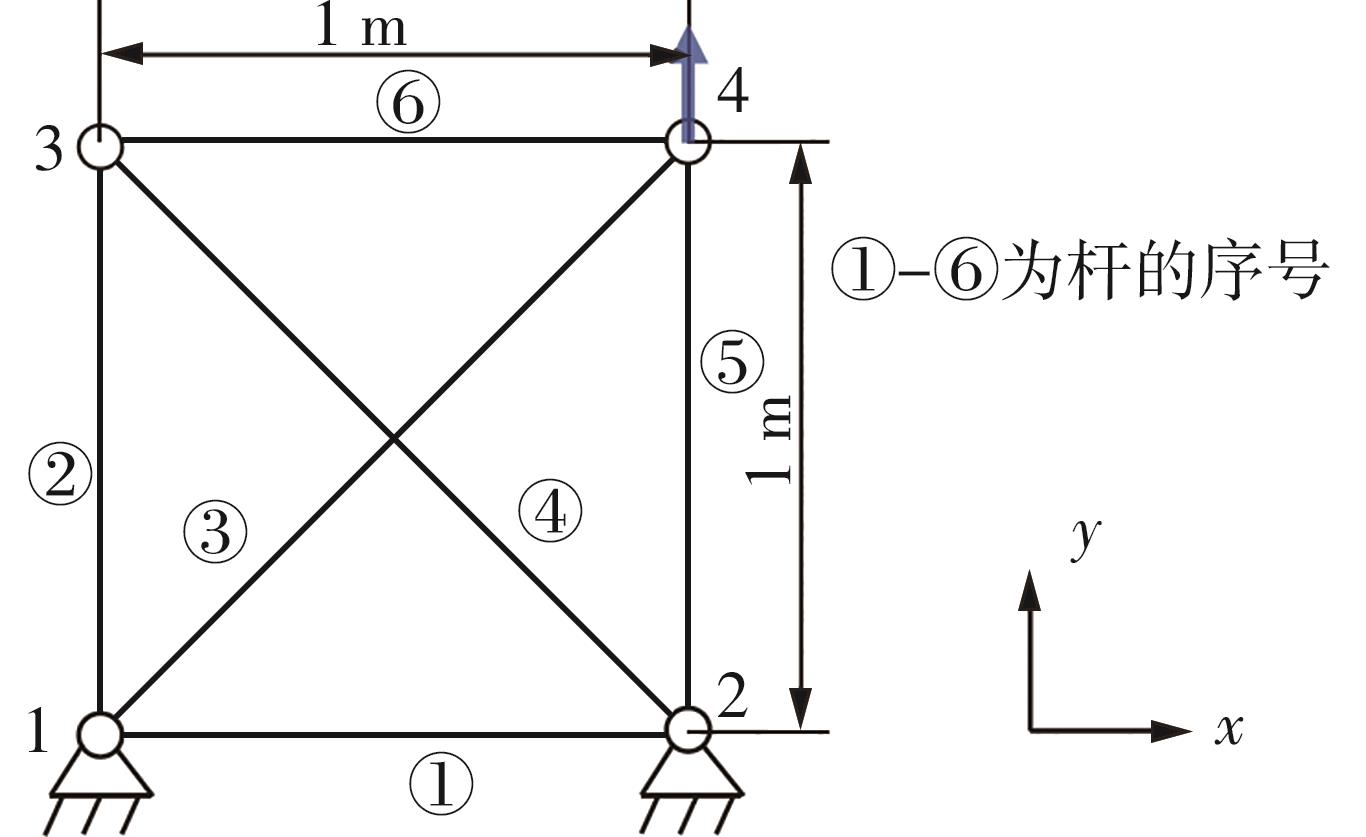
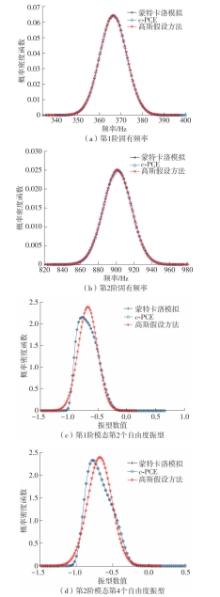
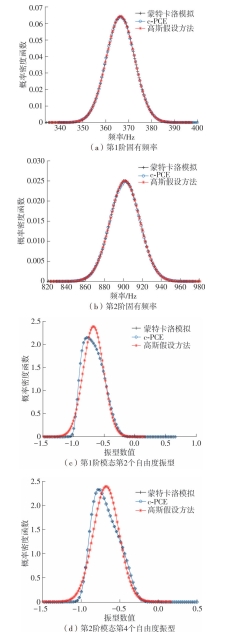
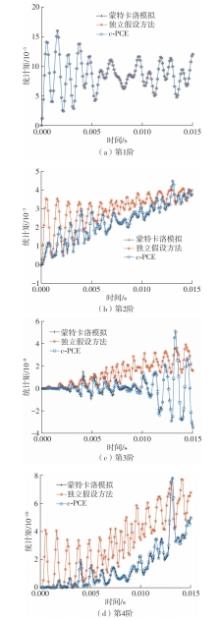
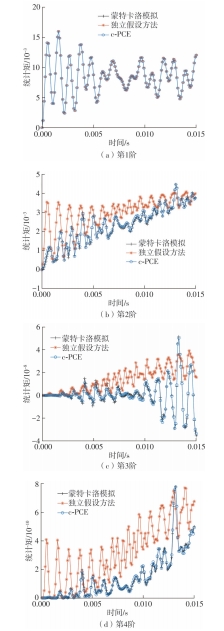
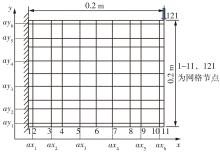
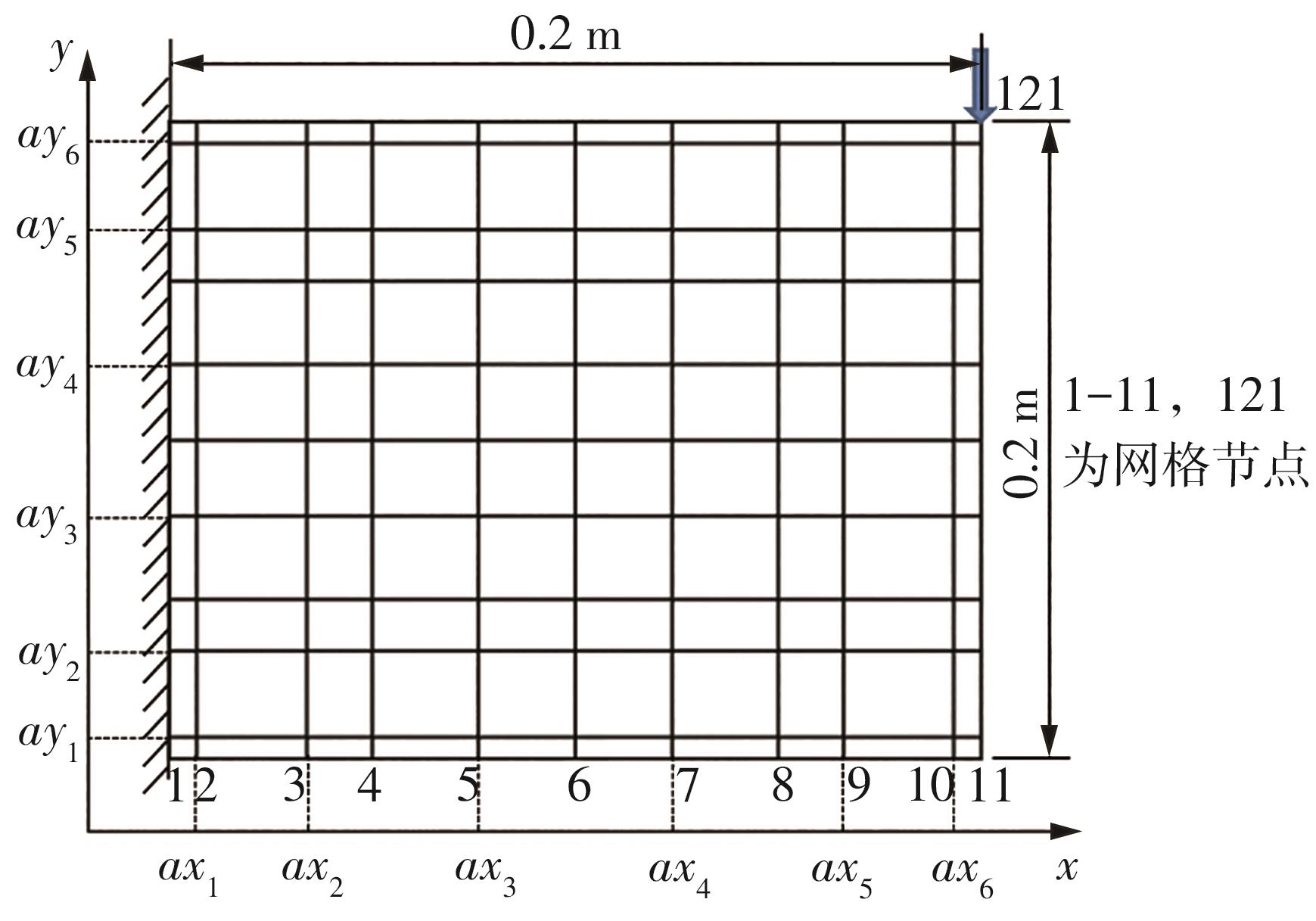
1	BATHE K J ．Finite element procedures［M］．Englewood Cliffs：Klaus-Jurgen Bathe，2006.
2	ALVIN K F， ROBERTSON A N， REICH G W，et al ．Structural system identification：from reality to models［J］．Computers & Structures，2003，81（12）：1149-1176.
3	YANG T， FAN S H， LIN C S ．Joint stiffness identification using FRF measurements［J］．Computers & Structures，2003，81（28/29）：2549-2556.
4	GOLLER B， BROGGI M， CALVI A，et al ．A stochastic model updating technique for complex aerospace structures［J］．Finite Elements in Analysis and Design，2011，47（7）：739-752.
5	YUEN K V， AU S K， BECK J L ．Two-stage structural health monitoring approach for phase i benchmark studies［J］．Journal of Engineering Mechanics-ASCE，2004，130（1）：16-33.
6	LAM H F， YIN T ．Statistical detection of multiple cracks on thin plates utilizing dynamic response［J］．Engineering Structures，2010，32（10）：3145-3152.
7	ZHU H P， LI L， HE X Q ．Damage detection method for shear buildings using the changes in the first mode shape slopes［J］．Computers & Structures，2011，89（9/10）：733-743.
8	SINGH B N， YADAV D， IYENGAR N G R ．Natural frequencies of composite plates with random material properties using higher-order shear deformation theory［J］．International Journal of Mechanical Sciences，2001，43（10）：2193-2214.
9	LIN S C ．The probabilistic approach for rotating Timoshenko beams［J］．International Journal of Solids and Structures，2001，38（40/41）：7197-7213.
10	VAN DEN NIEUWENHOF B， COYETT J P ．Modal approaches for the stochastic finite element analysis of structures with material and geometric uncertainties［J］．Computer Methods in Applied Mechanics and Engineering，2003，192（33/34）：3705-3729.
11	GAO W， ZHANG N， JI J ．A new method for random vibration analysis of stochastic truss structures［J］．Finite Elements in Analysis and Design，2009，45（3）：190-199.
12	GAO W， ZHANG N， DAI J ．A stochastic quarter-car model for dynamic analysis of vehicles with uncertain parameters［J］．Vehicle System Dynamics，2008，46（12）：1159-1169.
13	PEETERS B， DE R G ．Stochastic system identification for operational modal analysis：a review［J］．Journal of Dynamic Systems，Measurement and Control，2001，123（4）：659-667.
14	BRINCKER R， ZHANG L， ANDERSEN P ．Modal identification of output-only systems using frequency domain decomposition［J］．Smart Materials and Structures，2001，10（3）：441-445.
15	MAGALHAES F， CUNHA A ．Explaining operational modal analysis with data from an arch bridge［J］．Mechanical Systems and Signal Processing，2011，25（5）：1431-1450.
16	AU S K ．Fast bayesian ambient modal identification in the frequency domain，Part I：posterior most probable value［J］．Mechanical Systems and Signal Processing，2012，26（1）：60-75.
17	AU S K ．Fast bayesian ambient modal identification in the frequency domain，Part II：posterior uncertainty［J］．Mechanical Systems and Signal Processing，2012，26（1）：76-90.
18	AU S K， ZHANG F L， NI Y C ．Bayesian operational modal analysis：theory，computation，practice［J］．Computers & Structures，2013，126（28）：3-14.
19	BEHMANESH I， MOAVENI B， LOMBAERT G，et al ．Hierarchical bayesian model updating for structural identification［J］．Mechanical Systems and Signal Processing，2015（64/65）：360-376.
20	VANIK M W， BECK J L， AU S K ．Bayesian probabilistic approach to structural health monitoring［J］．Journal of Engineering Mechanics，2000，126（7）：738-745.
21	YUEN K V， BECK J L， KATAFYGIOTIS L S ．Efficient model updating and health monitoring methodology using incomplete modal data without mode matching［J］．Structural Control & Health Monitoring，2010，13（1）：91-107.
22	SOHN H， LAW K H ．A bayesian probabilistic approach for structure damage detection［J］．Earthquake Engineering & Structural Dynamics，2015，26（12）：1259-1281.
23	SAKAMOTO S， GHANEM R ．Polynomial chaos decomposition for the simulation of non-Gaussian nonstationary stochastic processes［J］．Journal of Engineering Mechanics，2002，128（2）：190-201.
24	PING M.H， HAN X， JIANG C，et al ．A time-variant uncertainty propagation analysis method based on a new technique for simulating non-Gaussian stochastic processes［J］．Mechanical Systems and Signal Processing，2021，150：107299.
25	XIONG F， Greene S， CHEN W，et al ．A new sparse grid based method for uncertainty propagation［J］．Structural and Multidisciplinary Optimization，2010，41（3）：335-349.
26	JIA X Y， JIANG C， FU C M，et al ．Uncertainty propagation analysis by an extended sparse grid technique［J］．Frontiers of Mechanical Engineering，2019，14（1）：33-46.
27	WU J， ZHANG D， JIANG C，et al ．On reliability analysis method through rotational sparse grid nodes［J］．Mechanical Systems and Signal Processing，147：107106.
28	GAO W， CHEN J， CUI M，et al ．Dynamic response analysis of linear stochastic truss structures under stationary random excitation［J］．Journal of Sound and Vibration，2005，281（1/2）：311-321.
29	XIU D， KARNIADAKIS G E ．The wiener--askey polynomial chaos for stochastic differential equations［J］．SIAM Journal on Scientific Computing，2002，24（2）：619-644.
30	ZHANG J， ELLINGWOOD B ．Orthogonal series expansions of random fields in reliability analysis［J］．Journal of Engineering Mechanics，1994，120（12）：2660-2677.
31	YANG C， DURAISWAMI R， GUMEROV N A，et al ．Improved fast gauss transform and efficient kernel density estimation［C］∥Proceedings of the Ninth IEEE International Conference on Computer Vision.［S.l.］：IEEE，2008.
32	KRISTAN M， LEONARDIS A， SKOCAJ D ．Multivariate online kernel density estimation with Gaussian kernels［J］．Pattern Recognition，2011，44（10/11）：2630-2642.

[1]	唐钱龙, 彭立敏, 邓锷, 等. 考虑随机场的盾构下穿条件下既有高铁交会行车安全性[J]. 华南理工大学学报(自然科学版), 2024, 52(4): 95-103.
[2]	郑思凡, 王卫星, 何占华, 等. 双粒度光流流形学习的刮刷总成摆杆摆幅检测[J]. 华南理工大学学报（自然科学版）, 2020, 48(1): 123-132.
[3]	孙季丰欧阳金华. 基于分块处理的条件随机场视频分割算法[J]. 华南理工大学学报(自然科学版), 2012, 40(6): 43-47.
[4]	闵华清吕居美罗荣华陈聪. 基于GMM 和MRF 的自适应阴影检测[J]. 华南理工大学学报（自然科学版）, 2011, 39(7): 115-120.
[5]	罗荣华闵华清. 用于移动机器人多目标跟踪的混合条件随机场[J]. 华南理工大学学报（自然科学版）, 2011, 39(5): 61-67.
[6]	苏成徐瑞范学明. 二维随机场离散的曲边单元局部平均法[J]. 华南理工大学学报（自然科学版）, 2008, 36(3): 104-107,120.
[7]	于江德樊孝忠尹继豪. 基于条件随机场的中文科研论文信息抽取[J]. 华南理工大学学报（自然科学版）, 2007, 35(9): 90-94,106.
[8]	许志良谢胜利. 一种基于MRF的自适应块效应去除算法[J]. 华南理工大学学报（自然科学版）, 2005, 33(7): 15-19.
[9]	苏成范学明颜全胜. 轴拉杆随机分析的域外奇点法[J]. 华南理工大学学报(自然科学版), 2003, 31(9): 86-89.

不确定性结构的非高斯模态参数模拟方法

Non-Gaussian Modal Parameters Simulation Methods for Uncertainty Structures

RichHTML

PDF

可视化

摘要/Abstract

引用本文

使用本文

图/表 11

参考文献 32

相关文章 9

编辑推荐

Metrics

本文评价