基于Matrix Core的高性能多维FFT设计与优化

doi:10.12141/j.issn.1000-565X.240035

华南理工大学学报(自然科学版) ›› 2025, Vol. 53 ›› Issue (3): 20-30.doi: 10.12141/j.issn.1000-565X.240035

基于Matrix Core的高性能多维FFT设计与优化

陆璐¹^,²(), 祝松祥¹, 田卿燕³, 林海山³, 郭逸劼¹

^1.华南理工大学计算机科学与工程学院，广东广州 510006
^2.鹏城实验室，广东深圳 518000
^3.广东省隧道工程安全与应急保障技术及装备企业重点实验室，广东广州 510440

收稿日期:2024-01-12 出版日期:2025-03-10 发布日期:2024-04-23
作者简介:陆璐（1971—），男，博士，教授，主要从事软件缺陷预测、高性能计算、深度学习训练推理加速研究。E-mail： lul@scut.edu.cn
基金资助:
广东省重点领域研发计划项目(2022B0101070001)

Design and Optimization of High-Performance Multi-Dimensional FFT Based on Matrix Core

LU Lu¹^,²(), ZHU Songxiang¹, TIAN Qingyan³, LIN Haishan³, GUO Yijie¹

^1.School of Computer Science and Engineering，South China University of Technology，Guangzhou 510006，Guangdong，China
^2.Pengcheng Laboratory，Shenzhen 518000，Guangdong，China
^3.Tunnel Engineering Safety and Emergency Support Technology and Equipment Laboratory of Guangdong Province，Guangzhou 510440，Guangdong，China

Received:2024-01-12 Online:2025-03-10 Published:2024-04-23
Supported by:
the Key-Area R & D Program of Guangdong Province(2022B0101070001)

摘要/Abstract

摘要：

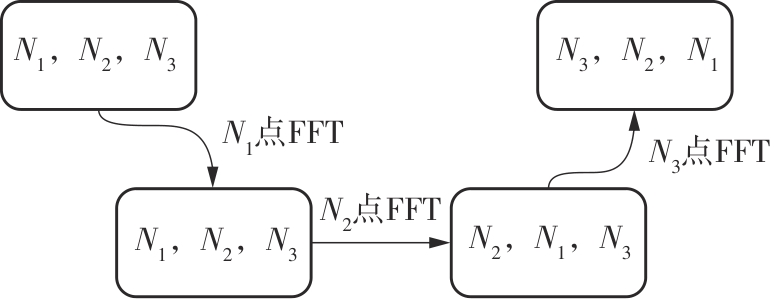
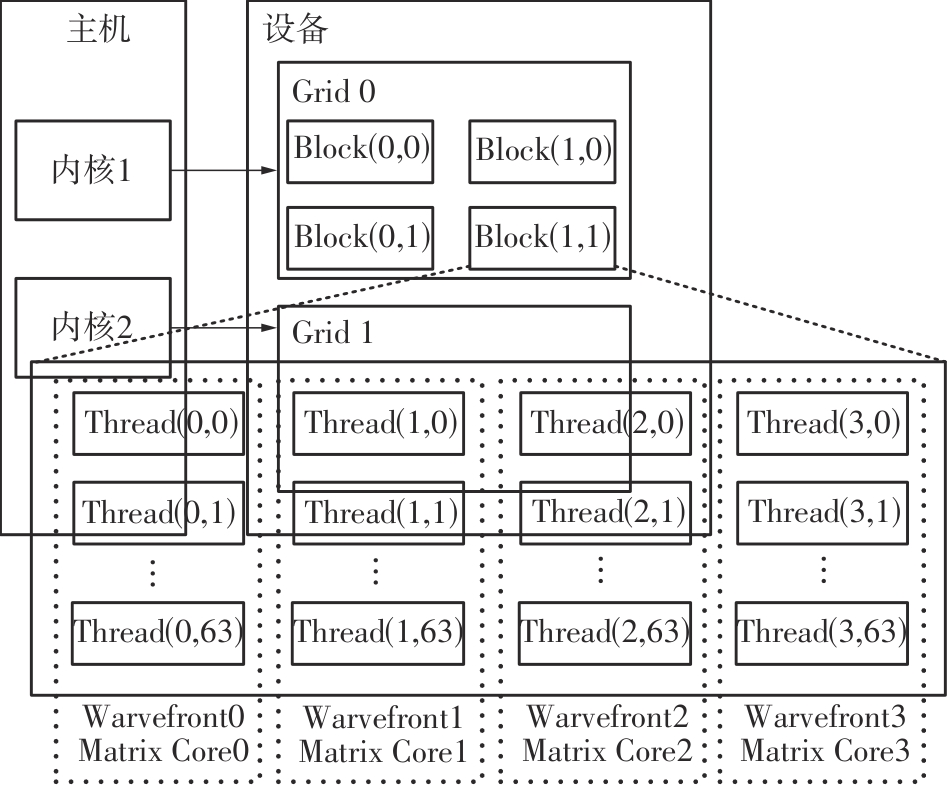
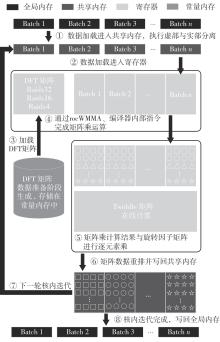
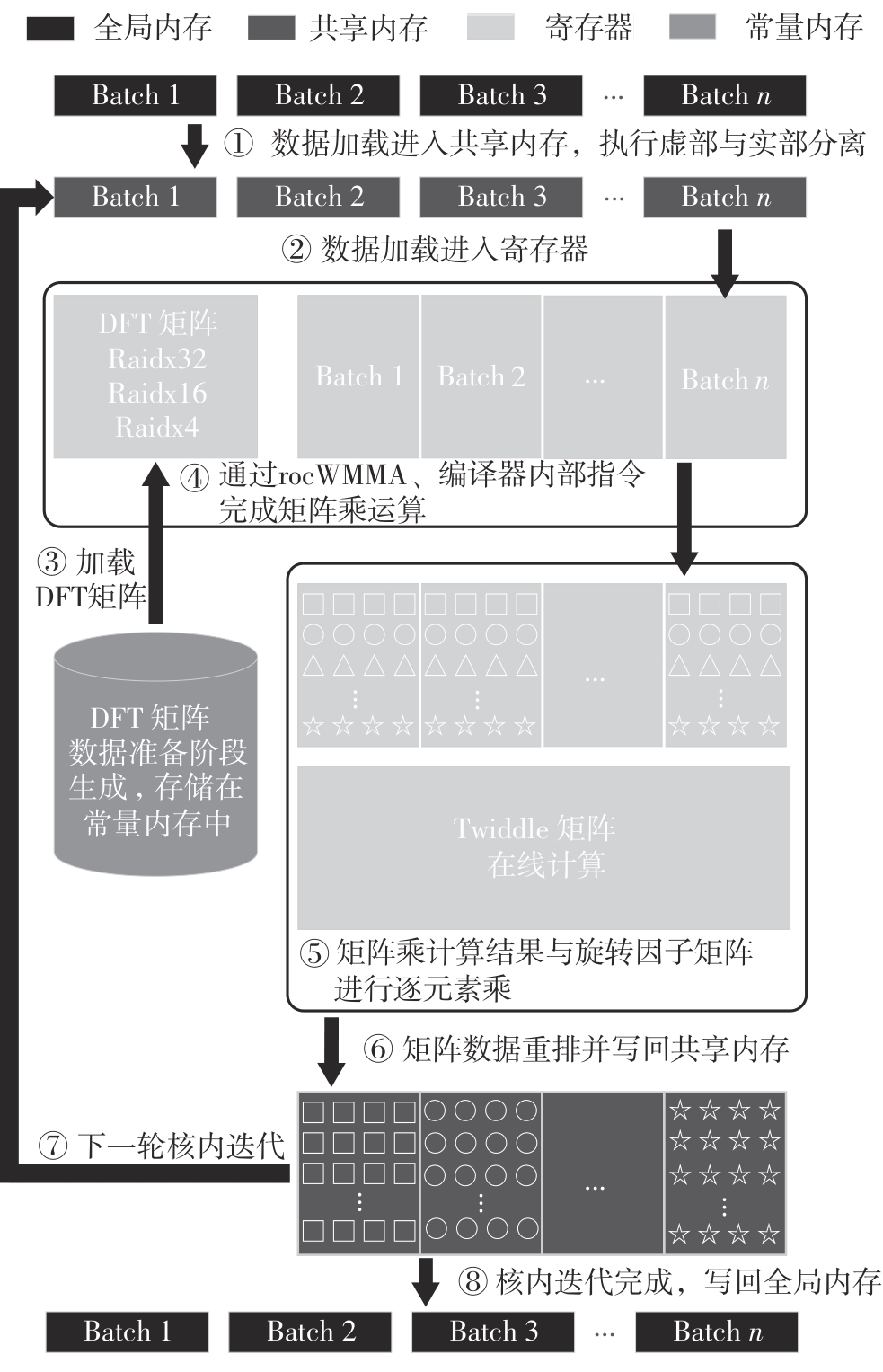
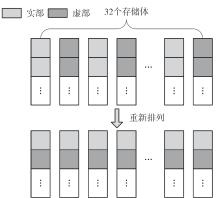
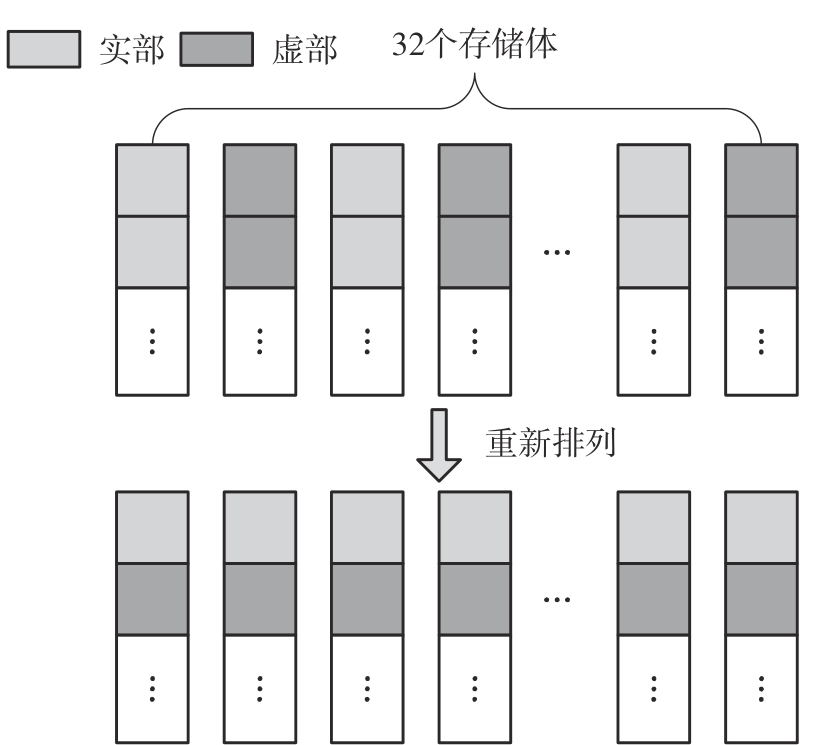
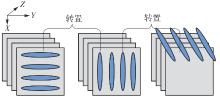
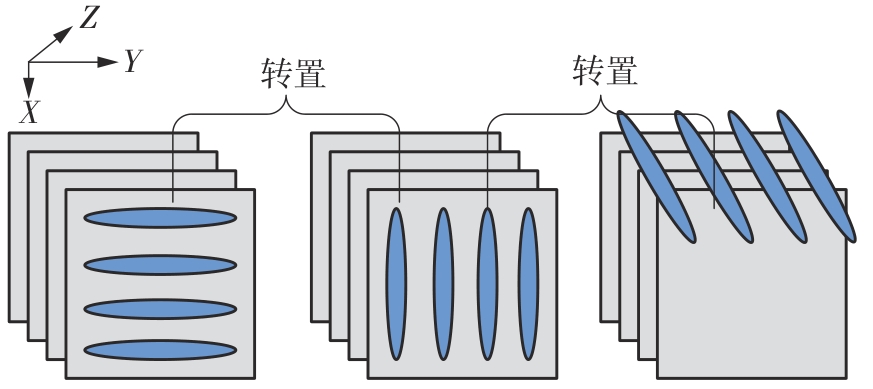
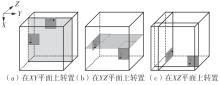
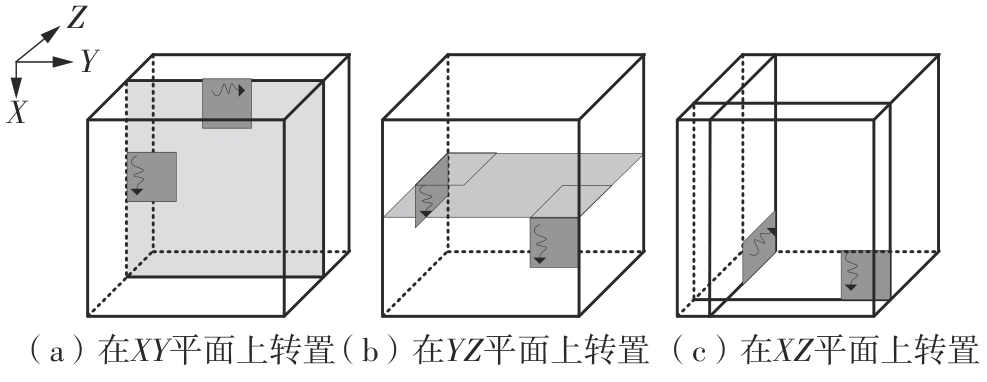
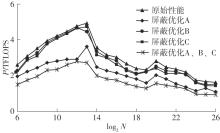
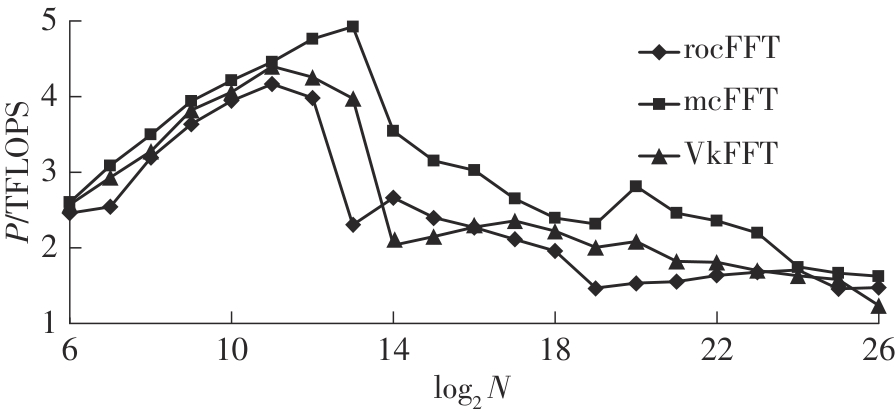
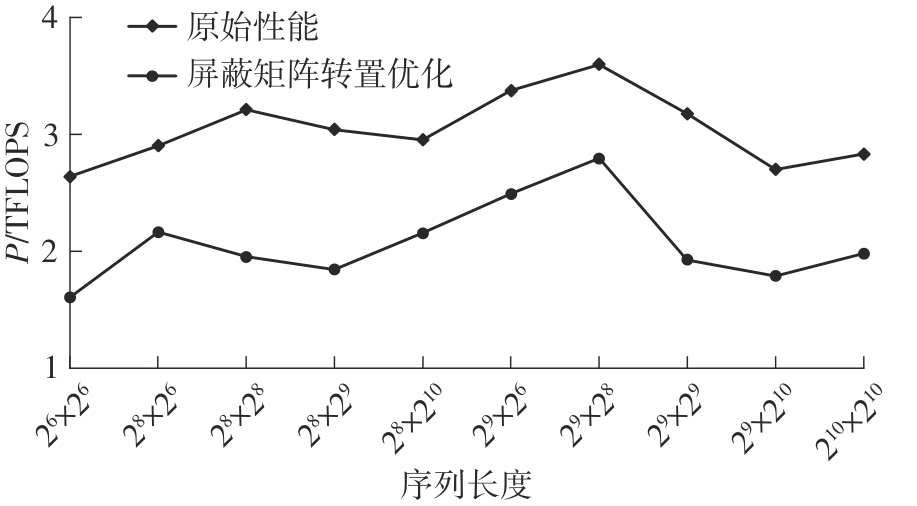
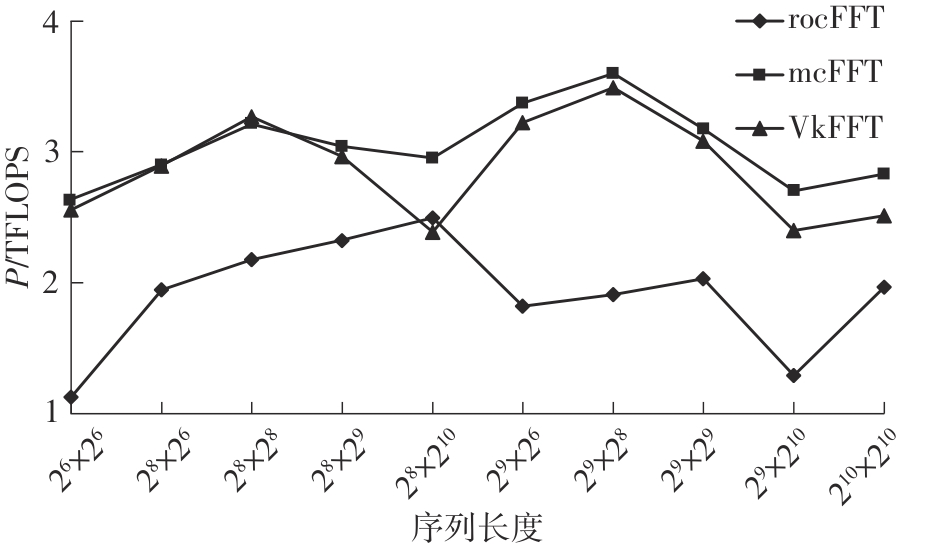
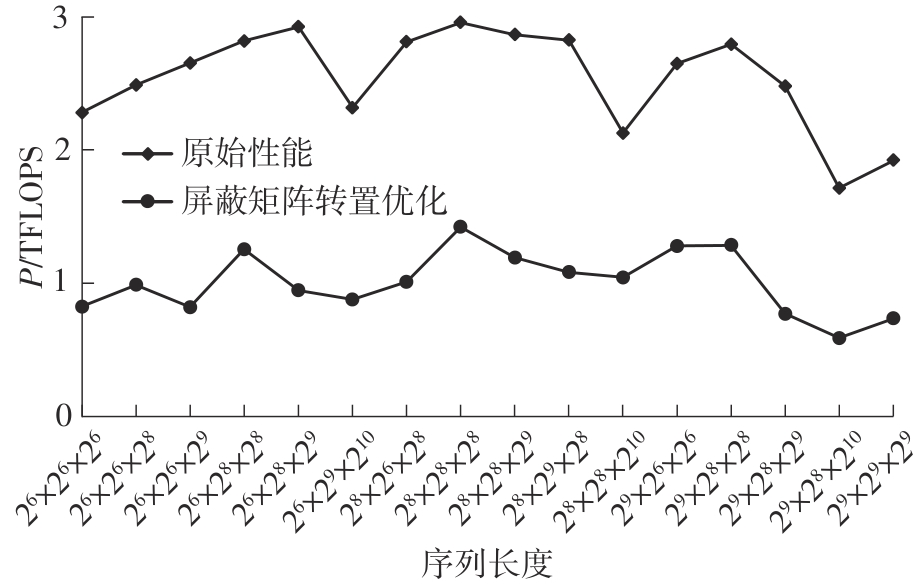
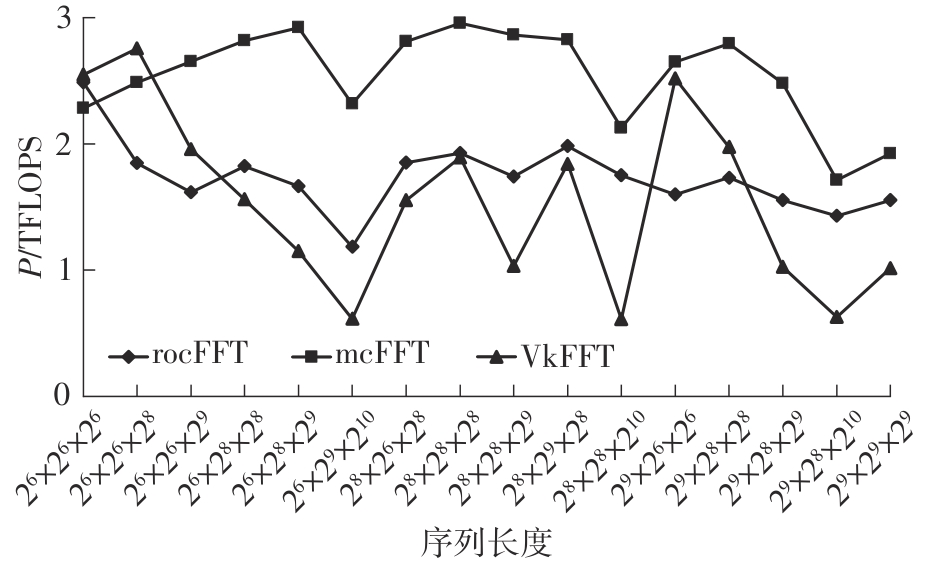
快速傅里叶变换（FFT）算法广泛应用于科学计算等领域。为了充分挖掘图形处理器（GPU）的计算能力并进一步提高FFT的计算效率，该文针对矩阵形式的Stockham FFT，提出了一种基于Matrix Core的高性能多维FFT计算方案。在计算优化方面，该方案利用Matrix Core加速FFT计算中的矩阵乘运算，同时通过编译器内部指令完成小粒度的矩阵乘加，使得Matrix Core支持更多尺寸的FFT计算。在内存优化方面，该方案使用2层迭代策略，以充分利用共享内存，减少与全局内存的数据交换；根据Matrix Core的矩阵数据在各个线程寄存器中的分布规律，直接在寄存器上完成FFT计算中大量存在的矩阵逐元素乘操作；通过对共享内存中的数据进行重排来缓解存储体冲突，并采用双缓冲策略缓解访存瓶颈。该文还提出了高效的矩阵转置策略，以加速多维FFT计算。在AMD MI250 GPU平台上将该方案与GPU上主流的高性能FFT计算库rocFFT和VkFFT进行了比较实验，结果表明：该方案在AMD MI250上的1维、2维和3维FFT平均计算效率均优于rocFFT和VkFFT，3维FFT的平均计算效率为rocFFT的1.5倍，为VkFFT的2.0倍，具有较好的性能提升；mcFFT的计算精度与rocFFT和VkFFT保持在相同水平。

关键词: 图形处理器, Matrix Core, 快速傅里叶变换, 矩阵乘法

Abstract:

Fast Fourier transform (FFT) algorithm finds widespread application in scientific computing and related fields. To fully leverage the computational power of the GPU and further enhance the performance of FFT calculations, this paper proposed a high-performance multi-dimensional FFT computation scheme based on the Matrix Core for the matrix form of Stockham FFT. In terms of computational optimization, this scheme utilizes Matrix Core to accelerate matrix multiplications in FFT computation while leveraging compiler intrinsic instructions to perform small-grained matrix multiply-accumulate operations, enabling Matrix Core to support FFT computations of more sizes. To minimize memory access, the proposed scheme directly performs matrix element-wise multiplication operations in the registers according to the distribution pattern of Matrix Core’s data across thread registers. It also mitigates bank conflicts by reordering data in shared memory, adopts a double-buffering strategy to alleviate access bottlenecks, and proposes an efficient matrix transposition strategy to accelerate multidimensional FFT computations. In this paper, the proposed scheme was compared to the well-known high-performance FFT computation libraries rocFFT and VkFFT on the AMD MI250 GPU platform. The results demonstrate that the proposed scheme outperforms rocFFT and VkFFT in terms of average computational performance for 1-dimensional, 2-dimensional, and 3-dimensional FFTs on the AMD MI250 GPU platform. For 3D FFT calculation, this method has an average performance that is 1.5 times faster than rocFFT and 2.0 times faster than VkFFT, demonstrating significant performance improvements.

Key words: graphics processing unit, Matrix Core, fast Fourier transform, matrix multiplication

中图分类号:

TP302.1

陆璐, 祝松祥, 田卿燕, 林海山, 郭逸劼. 基于Matrix Core的高性能多维FFT设计与优化[J]. 华南理工大学学报(自然科学版), 2025, 53(3): 20-30.

LU Lu, ZHU Songxiang, TIAN Qingyan, LIN Haishan, GUO Yijie. Design and Optimization of High-Performance Multi-Dimensional FFT Based on Matrix Core[J]. Journal of South China University of Technology(Natural Science Edition), 2025, 53(3): 20-30.

图/表 15

图1

图2

图3

图4

图5

图6

图7

图8

表1

图9

图10

图11

图12

图13

图14

参考文献 20

1	JUNG J， KOBAYASHI C， IMAMURA T，et al ．Parallel implementation of 3D FFT with volumetric decomposition schemes for efficient molecular dynamics simulations［J］．Computer Physics Communications，2016，200：57-65.
2	LOGESHWARAN N， VIJAYAPRADEEP S， KIM A R，et al ．Study of engineering electronic structure modulated non-noble metal oxides for scaled-up alkaline blend seawater splitting［J］．Journal of Energy Chemistry，2023，86：167-179.
3	MOHAPATRA B N， MOHAPATRA R K ．FFT and sparse FFT techniques and applications［C］∥ Procee-dings of 2017 the Fourteenth International Conference on Wireless and Optical Communications Networks．Mumbai：IEEE，2017：1-5.
4	DESPRÉS P， JIA X ．A review of GPU-based medical image reconstruction［J］．Physica Medica，2017，42：76-92.
5	CHI L， JIANG B， MU Y ．Fast Fourier convolution［C］∥ Advances in Neural Information Processing Systems 33：34th Conference on Advances in Neural Information Processing Systems．San Diego：Neural Information Proce-ssing Systems Foundation，Inc.，2020：4479-4488.
6	LUSZCZEK P， DONGARRA J J， KOESTER D，et al ．Introduction to the HPC challenge benchmark suite［R］．Denton：UNT Libraries Government Documents Department，2005：1-12.
7	LELIAERT J， MULKERS J ．Tomorrow’s micromagnetic simulations［J］．Journal of Applied Physics，2019，125（18）：180901/1-9.
8	MILOJICIC D ．Accelerators for artificial intelligence and high-performance computing［J］．Computer，2020， 53（2）：14-22.
9	TOLMACHEV D ．VkFFT：a performant，cross-platform and open-source GPU FFT library［J］．IEEE Access，2023，11：12039-12058.
10	ZHANG F，HU　C，YIN　Q，et al ．A GPU based memory optimized parallel method for FFT implementation［EB/OL］．（2017-07-23）［2024-01-12］．．
11	LEE J，KIM　D ．Large-scale 3D fast Fourier transform computation on a GPU［J］．ETRI Journal，2023，45（6）：1035-1045.
12	ZHAO Y， LIU F， MA W，et al ．MFFT：a GPU accelerated highly efficient mixed-precision large-scale FFT framework［J］．ACM Transactions on Architecture and Code Optimization，2023，20（3）：1-23.
13	NVIDIA Corporation ．NVIDIA Tesla V100 GPU architecture［EB/OL］．（2017-08-01）［2024-01-12］．.
14	SORNA A， CHENG X， D’AZEVEDO E，et al ．Optimizing the fast Fourier transform using mixed precision on tensor core hardware［C］∥ Proceedings of IEEE the 25th International Conference on High Performance Computing Workshops．Bengaluru：IEEE，2018：3-7.
15	DURRANI S， CHUGHTAI M S， HIDAYETOGLU M，et al ．Accelerating Fourier and number theoretic transforms using tensor cores and warp shuffles［C］∥ Proceedings of the 30th International Conference on Para-llel Architectures and Compilation Techniques．Atlanta：IEEE，2021：345-355.
16	PISHA L， LIGOWSKI L ．Accelerating non-power-of-2 size FOURIER transforms with GPU tensor cores［C］∥ Proceedings of 2021 IEEE International Parallel and Distributed Processing Symposium．Portland：IEEE，2021：507-516.
17	LI B， CHENG S， LIN J ．tcFFT：a fast half-precision FFT library for NVIDIA tensor cores［C］∥ Proceedings of 2021 IEEE International Conference on Cluster Compu-ting．Portland：IEEE，2021：1-11.
18	TUKEY C， COOLEY J ．An algorithm for the machine calculation of complex Fourier series［J］．Mathema-tics of Computation，1965，19（90）：297-301.
19	Advanced Micro Devices Inc． CDNA Introducing AMD 2 architecture［EB/OL］．（2021-09-21）［2024-01-12］．.
20	FRIGO M， JOHNSON S ．FFTW：an adaptive software architecture for the FFT［C］∥ Proceedings of the 1998 IEEE International Conference on Acoustics，Speech and Signal Processing．Seattle：IEEE，1998：1381-1384.

维度	平均相对误差
维度	VkFFT	rocFFT	mcFFT
1	4.398 156 × 10^-6	4.142 368 × 10^-6	3.892 482 × 10^-6
2	3.016 662 × 10^-6	3.113 926 × 10^-6	3.268 342 × 10^-6
3	2.204 218 × 10^-3	2.322 057 × 10^-3	2.121 653 × 10^-3

[1]	唐建焦向东戴波丁学鹏. 基于 1. 5 维谱估计的输油管道腐蚀超声回波信号分析[J]. 华南理工大学学报(自然科学版), 2019, 47(4): 120-126.
[2]	黄敏丁萍罗海飚. 共轭梯度法在 GPU 及 Xeon Phi 下的并行优化及比较[J]. 华南理工大学学报（自然科学版）, 2015, 43(11): 35-46,53.
[3]	李春雷韩强刘义捷肖栋梁. 螺旋曲杆中导波传播特性的有限元分析[J]. 华南理工大学学报（自然科学版）, 2014, 42(8): 6-13,33.
[4]	刘勇奚建清黄东平贾连印苗德成. 图形处理器上CSB⁺- 树索引的并行构建算法[J]. 华南理工大学学报（自然科学版）, 2014, 42(1): 123-127,134.
[5]	刘勇奚建清黄东平贾连印苗德成. 图形处理器上内存数据库索引T- 树的研究[J]. 华南理工大学学报（自然科学版）, 2013, 41(3): 22-28.
[6]	赵相坤李凤霞战守义. 基于GPU 的面向SPH 流体模拟的邻居查找算法[J]. 华南理工大学学报（自然科学版）, 2011, 39(7): 150-155.
[7]	周武胡跃明. 基于相位相关和重采样的亚像素图像配准算法[J]. 华南理工大学学报（自然科学版）, 2010, 38(10): 68-73,78.
[8]	张舞杰李迪叶峰. 基于视觉的贴片元件检测算法[J]. 华南理工大学学报（自然科学版）, 2010, 38(1): 65-69,86.
[9]	吴淑泉王前谢运祥. 适于消谐模型求解的矩阵乘法器设计与实现[J]. 华南理工大学学报(自然科学版), 2003, 31(8): 1-5.

基于Matrix Core的高性能多维FFT设计与优化

Design and Optimization of High-Performance Multi-Dimensional FFT Based on Matrix Core

RichHTML

PDF

可视化

摘要/Abstract

引用本文

使用本文

图/表 15

参考文献 20

相关文章 9

编辑推荐

Metrics

本文评价